题目内容
6.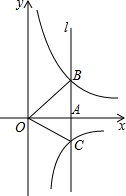 如图,经过点A(3,0)的直线l平行于y轴,与双曲线y=$\frac{4}{x}$和y=$\frac{k}{x}$分别交于点B和C.
如图,经过点A(3,0)的直线l平行于y轴,与双曲线y=$\frac{4}{x}$和y=$\frac{k}{x}$分别交于点B和C.(1)求点B的坐标;
(2)若△OBC的面积为3,求k的值.
分析 (1)由A(3,0),得到OA=3,根据点B在双曲线y=$\frac{4}{x}$上,AB⊥x轴,求得AB=$\frac{4}{3}$,于是得到结果;
(2)根据△OBC的面积为3,得到$\frac{1}{2}$BC•OA=3,求得BC=2,于是得到AC=$\frac{2}{3}$,求得|k|=AC•OA=2,即可得到结论.
解答 解:(1)∵A(3,0),
∴OA=3,
∵点B在双曲线y=$\frac{4}{x}$上,AB⊥x轴,
∴OA•AB=4,
∴AB=$\frac{4}{3}$,
∴B(3,$\frac{4}{3}$);
(2)∴△OBC的面积为3,
∴$\frac{1}{2}$BC•OA=3,
∴BC=2,
∴AC=$\frac{2}{3}$,
∴|k|=AC•OA=2,
∵k<0,
∴k=-2.
点评 本题考查了反比例函数系数k的几何意义,三角形面积的计算,熟记在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解题的关键.

练习册系列答案
相关题目
1. 右图是某几何体的三视图,这个几何体是( )
右图是某几何体的三视图,这个几何体是( )
 右图是某几何体的三视图,这个几何体是( )
右图是某几何体的三视图,这个几何体是( )| A. | 圆柱 | B. | 三棱柱 | C. | 球 | D. | 圆锥 |
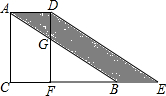 将直角三角形ABC沿CB方向平移CF的长度后,得到直角三角形DEF.已知DG=4,CF=6,AC=10,求阴影部分的面积.
将直角三角形ABC沿CB方向平移CF的长度后,得到直角三角形DEF.已知DG=4,CF=6,AC=10,求阴影部分的面积. 如图,AC∥CD,AP和CP分别平分∠BAC和∠ACD,过点P分别作PG⊥AC于点G,PE⊥AB于点E,EP的延长线交CD于点F.
如图,AC∥CD,AP和CP分别平分∠BAC和∠ACD,过点P分别作PG⊥AC于点G,PE⊥AB于点E,EP的延长线交CD于点F.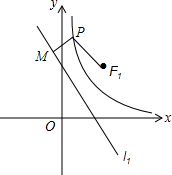 已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k).
已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k).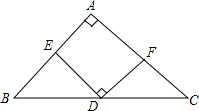 如下图,在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,ED⊥FD且分别交AB、AC于E、F.求证:BE=AF.
如下图,在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,ED⊥FD且分别交AB、AC于E、F.求证:BE=AF. 已知如图,在△ABC中,∠B=2∠C.
已知如图,在△ABC中,∠B=2∠C.
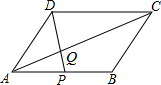 如图,在?ABCD中,点P在AB上,连结DP,交AC于点Q,当点P是AB的中点时,△ADQ的面积为1,则?ABCD的面积为( )
如图,在?ABCD中,点P在AB上,连结DP,交AC于点Q,当点P是AB的中点时,△ADQ的面积为1,则?ABCD的面积为( )