题目内容
5.已知方程ax2+bx+c=0的两实数根是a,c(ac≠0),则方程9cx2+3bx+a=0的根的情况是( )| A. | 必有一根为$\frac{1}{3}$ | B. | 必有一根为$\frac{1}{9}$ | ||
| C. | 两根分别为$\frac{1}{3}$,-$\frac{1}{3}$ | D. | 必有一根为$\frac{1}{3}$或-$\frac{1}{3}$ |
分析 根据根与系数的关系得a+c=-$\frac{b}{a}$,ac=$\frac{c}{a}$,由第二个等式可解出a=1或a=-1,讨论:当a=1时,易得b=-c-1,则方程9cx2+3bx+a=0化为9cx2+3(-c-1)x+1=0,利用因式分解法解得x1=$\frac{1}{3c}$,x2=$\frac{1}{3}$;当a=-1时,则b=c-1,方程9cx2+3bx+a=0化为9cx2+3(c-1)x-1=0,解得x1=-$\frac{1}{3c}$,x2=$\frac{1}{3}$,于是可判断方程9cx2+3bx+a=0一定有一根为$\frac{1}{3}$.
解答 解:∵方程ax2+bx+c=0的两实数根是a,c,
∴a+c=-$\frac{b}{a}$,ac=$\frac{c}{a}$,
∴a=1或a=-1,
当a=1时,1+c=-b,则b=-c-1,
∴方程9cx2+3bx+a=0化为9cx2+3(-c-1)x+1=0,
(3cx-1)(3x-1)=0,
∴x1=$\frac{1}{3c}$,x2=$\frac{1}{3}$;
当a=-1时,则b=c-1,
∴方程9cx2+3bx+a=0化为9cx2+3(c-1)x-1=0,
(3cx+1)(3x-1)=0,
∴x1=-$\frac{1}{3c}$,x2=$\frac{1}{3}$,
综上所述,方程9cx2+3bx+a=0一定有一根为$\frac{1}{3}$.
故选A.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了根与系数的关系.

练习册系列答案
相关题目
15. 如图,在菱形ABCD中,CG=DG,EF∥AC,HD∥EG.若EF:AC=1:3,则AH:EH等于( )
如图,在菱形ABCD中,CG=DG,EF∥AC,HD∥EG.若EF:AC=1:3,则AH:EH等于( )
 如图,在菱形ABCD中,CG=DG,EF∥AC,HD∥EG.若EF:AC=1:3,则AH:EH等于( )
如图,在菱形ABCD中,CG=DG,EF∥AC,HD∥EG.若EF:AC=1:3,则AH:EH等于( )| A. | 1:3 | B. | 1:2 | C. | 3:1 | D. | 2:1 |
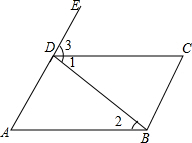 如图,填空
如图,填空
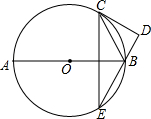 如图,AB为⊙O的直径,C为⊙O上一点,CD切⊙O于点C,BD⊥CD,BD交⊙O于点E,连CE.
如图,AB为⊙O的直径,C为⊙O上一点,CD切⊙O于点C,BD⊥CD,BD交⊙O于点E,连CE.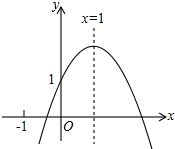 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )