题目内容
17.直线y=$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,将△AOB绕点B旋转90°,使点A落到点C处,则点C的坐标为(-3,7)或(3,-1).分析 先利用坐标轴上点的坐标特征求出A点和B点坐标,然后利用网格特征和旋转的性质求出△AOB绕点B顺时针或逆时针旋转90°后A的对应点C的坐标.
解答 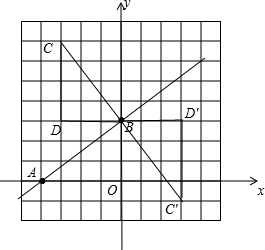 解:当x=0时,$\frac{3}{4}$x+3=0,解得x=-4,则A(4,0),
解:当x=0时,$\frac{3}{4}$x+3=0,解得x=-4,则A(4,0),
当y=0时,y=$\frac{3}{4}$x+3=3,则B(0,3),
如图,当△AOB绕点B顺时针旋转90°得到△CDB,C点坐标为(-3,7),
当△AOB绕点B顺时针旋转90°得到△C′D′B,C′点坐标为(3,-1).
故答案为(-3,7)或(3,-1).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
7.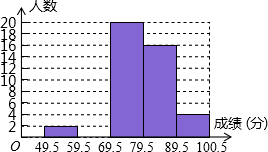 某班数学课代表小华对本班上学期期末考试数学成绩作了统计分析,绘制成如下频数、频率统计表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
某班数学课代表小华对本班上学期期末考试数学成绩作了统计分析,绘制成如下频数、频率统计表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
根据上述信息,完成下列问题:
(1)频数、频率统计表中,a=8;b=0.08;
(2)请将频数分布直方图补充完整;
(3)若成绩在79.5分以上为优秀,则该班优秀人数是多少?
 某班数学课代表小华对本班上学期期末考试数学成绩作了统计分析,绘制成如下频数、频率统计表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
某班数学课代表小华对本班上学期期末考试数学成绩作了统计分析,绘制成如下频数、频率统计表和频数分布直方图,请你根据图表提供的信息,解答下列问题:| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
(1)频数、频率统计表中,a=8;b=0.08;
(2)请将频数分布直方图补充完整;
(3)若成绩在79.5分以上为优秀,则该班优秀人数是多少?
5.已知方程ax2+bx+c=0的两实数根是a,c(ac≠0),则方程9cx2+3bx+a=0的根的情况是( )
| A. | 必有一根为$\frac{1}{3}$ | B. | 必有一根为$\frac{1}{9}$ | ||
| C. | 两根分别为$\frac{1}{3}$,-$\frac{1}{3}$ | D. | 必有一根为$\frac{1}{3}$或-$\frac{1}{3}$ |
12.下列说法中错误的是( )
| A. | 2是不等式x-3<8的解 | B. | -4不是不等式$\frac{1}{2}$x+2>0的解 | ||
| C. | -1是不等x≥-2的解 | D. | 不等式x>0和x≥0的解集相同 |
4. 请解答问题:
请解答问题:
(1)某种细胞分裂时由1个分裂成2个,2个分裂成4个,…一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x之间构成一个函数关系,请写出y与x之间的关系可以表示为y=2x;
(2)将此问题一般化,在定义域为全体实数时,试列表研究此函数的图象与性质:
(3)观察图象,请写出你认为正确的结论:①函数的图象是抛物线②函数的图象在一、二象限,y随x的增大而增大③函数图象经过(0,1)点,且与x轴没有交点.
 请解答问题:
请解答问题:(1)某种细胞分裂时由1个分裂成2个,2个分裂成4个,…一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x之间构成一个函数关系,请写出y与x之间的关系可以表示为y=2x;
(2)将此问题一般化,在定义域为全体实数时,试列表研究此函数的图象与性质:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y |
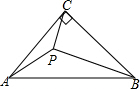 如图,在△ABC中,∠ACB=90°,AC=BC,P为三角形内部一点,且PC=3,PA=5,PB=7,则△PAB的面积为14.
如图,在△ABC中,∠ACB=90°,AC=BC,P为三角形内部一点,且PC=3,PA=5,PB=7,则△PAB的面积为14.