题目内容
13.△ABC中,AB=AC,点D为AC上一点,以CD为直径的半圆⊙O与AB相切于点E.
(1)如图①,若CD=3AD.求证:点E为AB的中点;
(2)如图②,作DF∥AB交半圆O于F,若AE=2BE=12,求DF的长.
分析 (1)连接OE,根据切线的性质得到∠OEA=90°根据勾股定理即可得到结论;
(2)连接OE,根据平行线的性质得到OE⊥DF,得到DG=$\frac{1}{2}DF$,根据勾股定理得到r=5,根据平行线分线段成比例定理即可得到结论.
解答 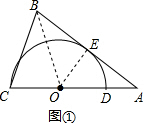 解:(1)连接OE,∵半圆⊙O与AB相切于点E,
解:(1)连接OE,∵半圆⊙O与AB相切于点E,
∴∠OEA=90°,
设OE=OC=OD=x,
∵CD=3AD,
∴AD=$\frac{2}{3}$x,
∴AC=AB=x+x+$\frac{2}{3}$x=$\frac{8}{3}$x,
∵AE=$\sqrt{A{O}^{2}-O{E}^{2}}$=$\sqrt{(x+\frac{2}{3}x)^{2}-{x}^{2}}$=$\frac{4}{3}$x,
∴AE=$\frac{1}{2}$AB,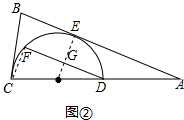
∴点E为AB的中点;
(2)连接OE交DF于G,连接OE,
∵AB切⊙O于E,
∴OE⊥AB,
∵DF∥AB,
∴OE⊥DF,
∴DG=$\frac{1}{2}DF$,
∵AE=2BE=12,
∴BE=6,
∵AB=AC,
∴AC=12+6=18,
设⊙O的半径为r,
∵OA2-OE2=AE2,
∴(18-r)2-r2=122,
∴r=5,
∵DF∥AB,
∴$\frac{GD}{AE}=\frac{OD}{OA}$,
∴$\frac{\frac{1}{2}DF}{12}=\frac{5}{13}$,
∴DF=$\frac{120}{13}$.
点评 本题考查了切线的性质,勾股定理,平行线分线段成比例定理.正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
4.下列由左到右的变形,是因式分解的是( )
| A. | (a+6)(a-6)=a2-36 | B. | x2-8x+16=(x-4)2 | ||
| C. | a2-b2+1=(a+b)(a-b)+1 | D. | (x-2)(x+3)=(x+3)(x-2) |
1.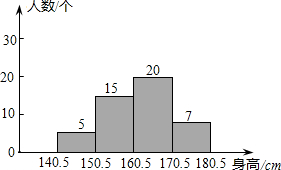 某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如图频数分布直方图,则下列说法正确的是( )
某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如图频数分布直方图,则下列说法正确的是( )
 某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如图频数分布直方图,则下列说法正确的是( )
某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如图频数分布直方图,则下列说法正确的是( )| A. | 该班人数最多的身高段的学生数为7人 | |
| B. | 该班身高最高段的学生数为7人 | |
| C. | 该班身高最高段的学生数为20人 | |
| D. | 该班身高低于160.5cm的学生数为15人 |
5.已知方程ax2+bx+c=0的两实数根是a,c(ac≠0),则方程9cx2+3bx+a=0的根的情况是( )
| A. | 必有一根为$\frac{1}{3}$ | B. | 必有一根为$\frac{1}{9}$ | ||
| C. | 两根分别为$\frac{1}{3}$,-$\frac{1}{3}$ | D. | 必有一根为$\frac{1}{3}$或-$\frac{1}{3}$ |
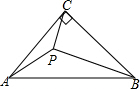 如图,在△ABC中,∠ACB=90°,AC=BC,P为三角形内部一点,且PC=3,PA=5,PB=7,则△PAB的面积为14.
如图,在△ABC中,∠ACB=90°,AC=BC,P为三角形内部一点,且PC=3,PA=5,PB=7,则△PAB的面积为14.