题目内容
12.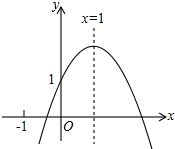 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
分析 根据图象与x轴交点的位置可以判断①错误,根据对称轴x=1可以判断②正确,根据增减性可以判断③错误,根据根与系数关系可以判断④正确.
解答 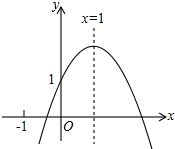 解:∵抛物线y=ax2+bx+c(a≠0)与x轴交于点(0,1),
解:∵抛物线y=ax2+bx+c(a≠0)与x轴交于点(0,1),
∴c=1,故①错误
∵对称轴x=1,
∴-$\frac{b}{2a}$=1,
∴2a+b=0,故②正确,
已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,
当x1>x2>1时,y1<y2,故③错误,
∵抛物线解析式为y=ax2-2ax+1,
∴两个根之和=2,
当一个根为3时,另一个根为-1,故④正确,
故选C.
点评 本题考查二次函数的图象与系数的关系,灵活应用二次函数图象的性质是解决问题的关键,属于中考常考题型.

练习册系列答案
相关题目
5.已知方程ax2+bx+c=0的两实数根是a,c(ac≠0),则方程9cx2+3bx+a=0的根的情况是( )
| A. | 必有一根为$\frac{1}{3}$ | B. | 必有一根为$\frac{1}{9}$ | ||
| C. | 两根分别为$\frac{1}{3}$,-$\frac{1}{3}$ | D. | 必有一根为$\frac{1}{3}$或-$\frac{1}{3}$ |
4. 请解答问题:
请解答问题:
(1)某种细胞分裂时由1个分裂成2个,2个分裂成4个,…一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x之间构成一个函数关系,请写出y与x之间的关系可以表示为y=2x;
(2)将此问题一般化,在定义域为全体实数时,试列表研究此函数的图象与性质:
(3)观察图象,请写出你认为正确的结论:①函数的图象是抛物线②函数的图象在一、二象限,y随x的增大而增大③函数图象经过(0,1)点,且与x轴没有交点.
 请解答问题:
请解答问题:(1)某种细胞分裂时由1个分裂成2个,2个分裂成4个,…一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x之间构成一个函数关系,请写出y与x之间的关系可以表示为y=2x;
(2)将此问题一般化,在定义域为全体实数时,试列表研究此函数的图象与性质:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y |
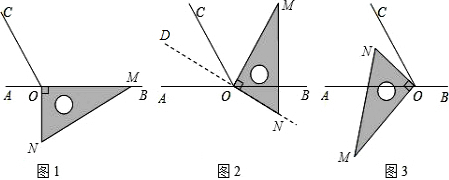
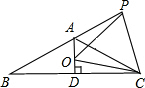 如图,在等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,若BC=2$\sqrt{3}$,AD=1,则S四边形AOCP=$\sqrt{3}$.
如图,在等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,若BC=2$\sqrt{3}$,AD=1,则S四边形AOCP=$\sqrt{3}$. (1)如图,工人师傅要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,使其圆心在线段AC上,且与AB、BC都相切.请你在图中画出这个半圆.(要求用直尺和圆规作图,保留作图痕迹,不要求写作法).
(1)如图,工人师傅要在一块形状为直角三角形(∠C为直角)的铁皮上裁出一个半圆形的铁皮,使其圆心在线段AC上,且与AB、BC都相切.请你在图中画出这个半圆.(要求用直尺和圆规作图,保留作图痕迹,不要求写作法).