题目内容
14.已知:关于x的一元二次方程x2+(n-2m)x+m2-mn=0①.(1)求证:方程①有两个实数根;
(2)若m-n-1=0,求证:方程①有一个实数根为1.
分析 (1)根据判别式△=(n-2m)2-4(m2-mn)≥0,然后根据判别式的意义即可得到结果;
(2)由已知得n=m-1,代入方程,将方程左边因式分解求x的值即可;
解答 解:(1)∵△=(n-2m)2-4(m2-mn)=n2-4mn+4m2-4m2+4mn=n2≥0,
∴方程①有两个实数根;
(2)证明:由已知得n=m-1,代入方程①,得
x2-(m+1)x+m2-m(m-1)=0,
整理,得x2-(m+1)x+m=0,即(x-1)(x-m)=0,
解得x1=1,x2=m,即方程①有一个实数根为1.
点评 此题主要考查了一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
4.已知a,b,c是实数且a>b,则下列不等式不成立的是( )
| A. | a+3>b+3 | B. | a-π>b-π | C. | ac2>bc2 | D. | $\frac{a}{{c}^{2}}$>$\frac{b}{{c}^{2}}$ |
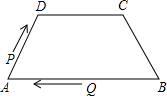 如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=11,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=11,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.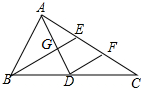 如图,在△ABC中,中线AD,BE相交于点G,过点D作DF∥BE交AC于点F,则$\frac{EF}{AC}$的值为$\frac{1}{4}$.
如图,在△ABC中,中线AD,BE相交于点G,过点D作DF∥BE交AC于点F,则$\frac{EF}{AC}$的值为$\frac{1}{4}$.