题目内容
2．已知2a+3b=1，求代数式2a2-a+2b-6b2-ab的值．分析 根据分组分解法，可得（2a2-ab-6b2）+（2b-a），根据提公因式法，可得答案．
解答 解：原式=（2a2-ab-6b2）+（2b-a）
=（a-2b）（2a+3b）-（a-2b）
=（a-2b）[（2a+3b）-1]
=（a-2b）（2a+3b-1），
当2a+3b=1时，原式=（a-2b）（1-1）=0．
点评 本题考查了因式分解的应用，利用分组法分解因式得出（a-2b）（2a+3b）-（a-2b）是解题关键．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
13．下列不是无理数的是（ ）
| A． | $\sqrt{4}$ | B． | 3.141141114… | C． | $\sqrt{3}$ | D． | π |
10．下列说法正确的是（ ）
| A． | 25的平方根是5 | B． | -22的算术平方根是2 | ||
| C． | 0.8的立方根是0.2 | D． | $\frac{5}{6}$ 是$\frac{25}{36}$的一个平方根 |
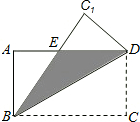如图，在矩形ABCD中，AB=3，BC=4，如果将该矩形沿对角线BD重叠．