题目内容
6.若a,b是有理数,且a$\sqrt{2}$+b$\sqrt{\frac{1}{2}}$+3=a+b,试求ab的值.分析 根据已知等式,以及a,b为有理数,确定出a与b的值,即可求出ab的值.
解答 解:已知等式整理得:(a+$\frac{1}{2}$b)$\sqrt{2}$+3=a+b,
可得$\left\{\begin{array}{l}{a+\frac{1}{2}b=0}\\{a+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-3}\\{b=6}\end{array}\right.$,
则ab=-18.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知如图,在?ABCD中,BF⊥AD、BE⊥DC,垂足分别是F、E,∠EDF=30°,BE=8,BF=14,则?ABCD的周长是88.
已知如图,在?ABCD中,BF⊥AD、BE⊥DC,垂足分别是F、E,∠EDF=30°,BE=8,BF=14,则?ABCD的周长是88.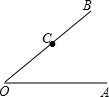 我市规划局要新建两条马路,如图所示,准备过游乐场C修一条与OA平行的马路,这条马路与∠AOB的平分线有一交点D,计划再OA边上建一个购物商场E,且使D到E最近,请利用量角器和三角板画出图形.
我市规划局要新建两条马路,如图所示,准备过游乐场C修一条与OA平行的马路,这条马路与∠AOB的平分线有一交点D,计划再OA边上建一个购物商场E,且使D到E最近,请利用量角器和三角板画出图形.