题目内容
4.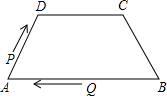 如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=11,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=11,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
分析 根据平行四边形的判定可得CP=BQ,四边形PQBC为平行四边形,设运动时间为x秒,表示出CP和BQ的长,然后可得关于x的方程,再解即可.
解答  解:当P在DC边上,PC=BQ,四边形PQBC为平行四边形,
解:当P在DC边上,PC=BQ,四边形PQBC为平行四边形,
设运动时间为x秒,则CP=12-3x,BQ=x,
故12-3x=x,
解得:x=3,
故答案为:3.
点评 此题主要考查了平行四边形的判定,关键是掌握一组对边平行且相等的四边形是平行四边形.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14.下列计算中正确的是( )
| A. | $\sqrt{m^2}+\sqrt{n^2}=\sqrt{{m^2}+{n^2}}$ | B. | $\sqrt{{a^2}-{b^2}}=\sqrt{a^2}-\sqrt{b^2}=a-b$ | ||
| C. | $\sqrt{3}×\sqrt{2}=\sqrt{3×2}$ | D. | $\sqrt{{{({-3})}^2}}=-3$ |
13.下列不是无理数的是( )
| A. | $\sqrt{4}$ | B. | 3.141141114… | C. | $\sqrt{3}$ | D. | π |
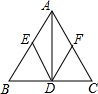 如图,在△ABC中,点D是BC的中点,DE∥AC,DF∥AB.
如图,在△ABC中,点D是BC的中点,DE∥AC,DF∥AB. 已知如图,在?ABCD中,BF⊥AD、BE⊥DC,垂足分别是F、E,∠EDF=30°,BE=8,BF=14,则?ABCD的周长是88.
已知如图,在?ABCD中,BF⊥AD、BE⊥DC,垂足分别是F、E,∠EDF=30°,BE=8,BF=14,则?ABCD的周长是88.