题目内容
9.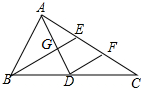 如图,在△ABC中,中线AD,BE相交于点G,过点D作DF∥BE交AC于点F,则$\frac{EF}{AC}$的值为$\frac{1}{4}$.
如图,在△ABC中,中线AD,BE相交于点G,过点D作DF∥BE交AC于点F,则$\frac{EF}{AC}$的值为$\frac{1}{4}$.
分析 根据三角形中位线定理得到EF=FC,根据重心的性质和平行线的性质得到AE=2EF,计算得到答案.
解答 解:∵DF∥BE,BD=DC,
∴EF=FC,
∵G是△ABC的重心,
∴AG=2GD,又DF∥BE,
∴AE=2EF,
∴$\frac{EF}{AC}$=$\frac{1}{4}$,
故答案为:$\frac{1}{4}$.
点评 本题考查的是三角形中位线定理和三角形的重心的概念和性质,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
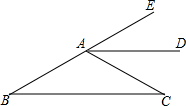 如图,已知∠B=∠C,AD∥BC.
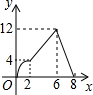
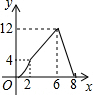
如图,已知∠B=∠C,AD∥BC. 如图,矩形ABCD的边AB=4,BC=8,点P从A出发,以每秒2个单位沿A-B-C-D运动,同时点Q也从A出发,以每秒1个单位沿A-D运动,△APQ的面积为y,运动的时间为x秒,则y关于x的函数图象为( )
如图,矩形ABCD的边AB=4,BC=8,点P从A出发,以每秒2个单位沿A-B-C-D运动,同时点Q也从A出发,以每秒1个单位沿A-D运动,△APQ的面积为y,运动的时间为x秒,则y关于x的函数图象为( )