题目内容
19.已知m2+m-4=0,$\frac{1}{{n}^{2}}$$+\frac{1}{n}$-4=0,m,n为实数,且m≠$\frac{1}{n}$,则m+$\frac{1}{n}$=-1.分析 可把m、$\frac{1}{n}$看作方程x2+x-4=0的两根,根据根与系数的关系得到m+$\frac{1}{n}$=-1即可.
解答 解:∵m≠$\frac{1}{n}$,∴m、$\frac{1}{n}$看作方程x2+x-4=0的两根,
∴m+$\frac{1}{n}$=-1.
故答案为:-1.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
10.下列说法正确的是( )
| A. | 25的平方根是5 | B. | -22的算术平方根是2 | ||
| C. | 0.8的立方根是0.2 | D. | $\frac{5}{6}$ 是$\frac{25}{36}$的一个平方根 |
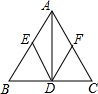 如图,在△ABC中,点D是BC的中点,DE∥AC,DF∥AB.
如图,在△ABC中,点D是BC的中点,DE∥AC,DF∥AB.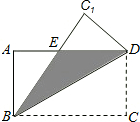 如图,在矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD重叠.
如图,在矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD重叠.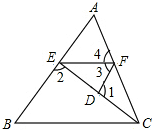 如图,已知∠1+∠2=180°,∠3=∠B,∠4=60°,求∠ACB的度数.
如图,已知∠1+∠2=180°,∠3=∠B,∠4=60°,求∠ACB的度数.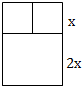 一根木料长为42米,要做一个如图的窗框,已知上框架与下框架高的比为1:2,求:
一根木料长为42米,要做一个如图的窗框,已知上框架与下框架高的比为1:2,求: