题目内容
19.如果6m=a,那么我们称m为a的郎格数,记为m=f(a).有上述定义可知:6m=a和m=f(a)中的变量a与m所表示的关系为同一关系,并且有性质:若a、b均为正数,则f(ab)=f(a)+f(b),f($\frac{a}{b}$)=f(a)-f(b).(1)根据郎格数的定义可得:
f(6)=1;f($\frac{1}{6}$)=-1;f($\frac{1}{36}$)=-2;
(2)根据郎格数的性质可得:
$①\frac{f({a}^{a})}{f(a)}$=a(a为正数)
②若f(2)=x(x≠0),则f(3)=1-x,f(4)=2x.
(3)若下表中与数a对应的郎格数f(a)有且只有一个是不正确的,请找出错误的郎格数,说明理由并改正.
| a | 1.5 | 3 | 4 | 9 | 16 | 24 |
| f(a) | 2x+y | $\frac{1+2x+y}{2}$ | 1-2x-y | 1+2x+y | 2-4x-2y | -2x-y |
分析 (1)根据定义由61=6、6-1=$\frac{1}{6}$、6-2=$\frac{1}{36}$可得f(6)、f($\frac{1}{6}$)、f($\frac{1}{36}$)的值;
(2)①将$\frac{f({a}^{a})}{f(a)}$根据性质写成$\frac{f(a)+f(a)+…+f(a)}{f(a)}$可得;
②根据性质将f(3)写成f($\frac{6}{2}$)=f(6)-f(2),f(4)写成f(2×2)=f(2)+f(2)可得;
(3)分别假设f(3)≠$\frac{1+2x+y}{2}$、f(4)≠1-2x-y推得f(9)、f(16),根据有且只有一个错误可排除这四个,再根据以上f(6)、f(4)的值推出f(1.5)、f(24),即可判断.
解答 解:(1)根据定义,∵61=6,∴f(6)=1;
∵6-1=$\frac{1}{6}$,∴f($\frac{1}{6}$)=-1;
∵6-2=$\frac{1}{36}$,∴f($\frac{1}{36}$)=-2.
(2)$①\frac{f({a}^{a})}{f(a)}$=$\frac{f(a•a•…•a)}{f(a)}$=$\frac{f(a)+f(a)+…+f(a)}{f(a)}$=$\frac{af(a)}{f(a)}$=a;
②∵f(2)=x(x≠0),
∴f(3)=f($\frac{6}{2}$)=f(6)-f(2)=1-x;
f(4)=f(2×2)=f(2)+f(2)=2x.
(3)假设f(3)≠$\frac{1+2x+y}{2}$,则有f(9)=f(3×3)=f(3)+f(3)=2f(3)≠1+2x+y.
∵有且只有一个错误,
∴f(3)=$\frac{1+2x+y}{2}$,f(9)=1+2x+y都是正确的.
假设f(4)≠1-2x-y,则有f(16)=f(4×4)=f(4)+f(4)=2f(4)≠2-4x-2y.
∵有且只有一个错误,
∴f(4)=1-2x-y,f(16)=2-4x-2y都是正确的.
∵f(6)=1,
∴f(1.5)=f($\frac{6}{4}$)=1-(1-2x-y)=2x+y,
f(24)=f(4×6)=f(4)+f(6)=1-2x-y+1=2-2x-y≠-2x-y,
∴f(24)=-2x-y是不正确的,
f(24)应为2-2x-y.
故答案为:(1)1,-1,-2;(2)①a,②1-x,2x.
点评 本题主要考查整式的运算和新定义下的定义及性质得运用,结合题目运用性质进行变形求值是本题的根本,利用已求式子的值作为已知条件再加以运用是解题的一种手段.

 阅读快车系列答案
阅读快车系列答案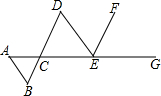 如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )| A. | 0个 | B. | 1个 | C. | 3个 | D. | 5个 |
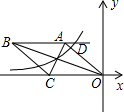 如图,在平面直角坐标系中,菱形OABC的一边在x轴上,反比例函数y-$\frac{k}{x}$(k≠0)的图象经过菱形两对交线的交点,且与AB所在直线交于点D,已知AC•OB=64$\sqrt{2}$,OC=8,则以下结论:①k=-16$\sqrt{2}$;②点D的纵坐标为4$\sqrt{2}$;③∠OBC=22.5°;④反比例函数y=-$\frac{k}{x}$随x的增大而增大;⑤tan∠AOC=1,其中正确的是( )
如图,在平面直角坐标系中,菱形OABC的一边在x轴上,反比例函数y-$\frac{k}{x}$(k≠0)的图象经过菱形两对交线的交点,且与AB所在直线交于点D,已知AC•OB=64$\sqrt{2}$,OC=8,则以下结论:①k=-16$\sqrt{2}$;②点D的纵坐标为4$\sqrt{2}$;③∠OBC=22.5°;④反比例函数y=-$\frac{k}{x}$随x的增大而增大;⑤tan∠AOC=1,其中正确的是( )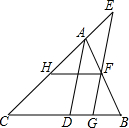 如图,已知∠ADB+∠EGC=180°,AD平分∠BAC,HF∥BC.
如图,已知∠ADB+∠EGC=180°,AD平分∠BAC,HF∥BC.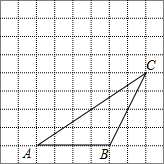 如下图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′、中线A′E.
如下图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′、中线A′E.