题目内容
7.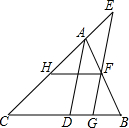 如图,已知∠ADB+∠EGC=180°,AD平分∠BAC,HF∥BC.
如图,已知∠ADB+∠EGC=180°,AD平分∠BAC,HF∥BC.(1)∠AFE与∠E相等吗?判断并说明理由;
(2)若∠ADB=78°,求∠HFG的度数.
分析 (1)根据同旁内角互补,两直线平行,得出AD∥EG,再根据两直线平行同位角相,内错角相等得出∠CAD=∠E,∠DAB=∠AFE,最后根据角平分线的性质得出∠CAD=∠DAB,从而得出∠AFE=∠E;
(2)根据AD∥EG,得出∠ADB=∠EGB,再根据HF∥BC,得出∠HFG=∠EGB,从而得出∠ADB=∠HFG,再根据∠ADB=78°,即可得出∠HFG的度数.
解答 解:(1)∵∠ADB+∠EGC=180°,
∴AD∥EG,
∴∠CAD=∠E,∠DAB=∠AFE,
∵AD平分∠BAC,
∴∠CAD=∠DAB,
∴∠AFE=∠E;
(2)∵AD∥EG,
∴∠ADB=∠EGB,
∵HF∥BC,
∴∠HFG=∠EGB,
∴∠ADB=∠HFG,
∵∠ADB=78°,
∴∠HFG=78°.
点评 此题考查了平行线的判定与性质,用到的知识点为:同旁内角互补,两直线平行;两直线平行,内错角相等,同位角相等.

练习册系列答案
相关题目
17.钓鱼岛是位于中国东海钓鱼岛列岛的主岛,自古以来都是中国的领土,其周围的海域面积约为170000平方公里,170000用科学记数法可表示为( )
| A. | 0.17×106 | B. | 1.7×105 | C. | 1.7×106 | D. | 17×104 |
12.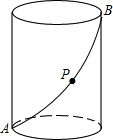 如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )
如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )
 如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )
如图,圆柱底面半径为4cm,高为8cm,动点P从点A出发,沿着圆柱的侧面移动到点B的最短距离为( )| A. | 2$\sqrt{{π}^{2}+4}$cm | B. | 4$\sqrt{{π}^{2}+4}cm$ | C. | 8$\sqrt{{π}^{2}+4}cm$ | D. | 无法确定 |
19.如果6m=a,那么我们称m为a的郎格数,记为m=f(a).有上述定义可知:6m=a和m=f(a)中的变量a与m所表示的关系为同一关系,并且有性质:若a、b均为正数,则f(ab)=f(a)+f(b),f($\frac{a}{b}$)=f(a)-f(b).
(1)根据郎格数的定义可得:
f(6)=1;f($\frac{1}{6}$)=-1;f($\frac{1}{36}$)=-2;
(2)根据郎格数的性质可得:
$①\frac{f({a}^{a})}{f(a)}$=a(a为正数)
②若f(2)=x(x≠0),则f(3)=1-x,f(4)=2x.
(3)若下表中与数a对应的郎格数f(a)有且只有一个是不正确的,请找出错误的郎格数,说明理由并改正.
(1)根据郎格数的定义可得:
f(6)=1;f($\frac{1}{6}$)=-1;f($\frac{1}{36}$)=-2;
(2)根据郎格数的性质可得:
$①\frac{f({a}^{a})}{f(a)}$=a(a为正数)
②若f(2)=x(x≠0),则f(3)=1-x,f(4)=2x.
(3)若下表中与数a对应的郎格数f(a)有且只有一个是不正确的,请找出错误的郎格数,说明理由并改正.
| a | 1.5 | 3 | 4 | 9 | 16 | 24 |
| f(a) | 2x+y | $\frac{1+2x+y}{2}$ | 1-2x-y | 1+2x+y | 2-4x-2y | -2x-y |
17.如图,已知△ABC的三条边和三个角六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
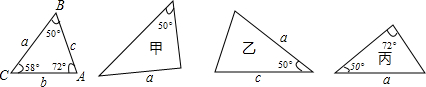
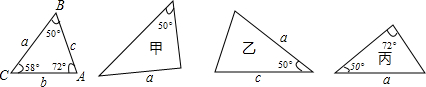
| A. | 只有乙 | B. | 只有丙 | C. | 甲和乙 | D. | 乙和丙 |
 如图,正方形ODBC中,OB=$\sqrt{2}$,OA=OB,则数轴上点A表示的数是-$\sqrt{2}$.
如图,正方形ODBC中,OB=$\sqrt{2}$,OA=OB,则数轴上点A表示的数是-$\sqrt{2}$.