题目内容
9.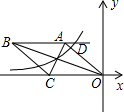 如图,在平面直角坐标系中,菱形OABC的一边在x轴上,反比例函数y-$\frac{k}{x}$(k≠0)的图象经过菱形两对交线的交点,且与AB所在直线交于点D,已知AC•OB=64$\sqrt{2}$,OC=8,则以下结论:①k=-16$\sqrt{2}$;②点D的纵坐标为4$\sqrt{2}$;③∠OBC=22.5°;④反比例函数y=-$\frac{k}{x}$随x的增大而增大;⑤tan∠AOC=1,其中正确的是( )
如图,在平面直角坐标系中,菱形OABC的一边在x轴上,反比例函数y-$\frac{k}{x}$(k≠0)的图象经过菱形两对交线的交点,且与AB所在直线交于点D,已知AC•OB=64$\sqrt{2}$,OC=8,则以下结论:①k=-16$\sqrt{2}$;②点D的纵坐标为4$\sqrt{2}$;③∠OBC=22.5°;④反比例函数y=-$\frac{k}{x}$随x的增大而增大;⑤tan∠AOC=1,其中正确的是( )| A. | ①③⑤ | B. | ②③⑤ | C. | ②③④⑤ | D. | ①②③④⑤ |
分析 延长BA交y轴于点H,过点E作EF⊥OC于点F.①运用菱形的面积公式可求出△ECO的面积,根据△EFO的面积小于△ECO的面积可解决问题;②要求点D的纵坐标,只需根据菱形的面积公式(底乘以高)求出OH即可;③只需解直角三角形OHA,就可求出∠AOH,即可得到∠AOC,再根据菱形的性质,就可求出∠OBC;④只需根据k的符号,就可确定反比例函数y=-$\frac{k}{x}$的增减性;⑤根据∠AOC的度数即可得到tan∠AOC的值.
解答 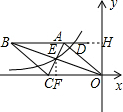 解:延长BA交y轴于点H,过点E作EF⊥OC于点F,如图.
解:延长BA交y轴于点H,过点E作EF⊥OC于点F,如图.
①∵四边形OABC是菱形,
∴S菱形OABC=$\frac{1}{2}$AC•OB=$\frac{1}{2}$×64$\sqrt{2}$=32$\sqrt{2}$,
∴S△ECO=$\frac{1}{4}$S菱形OABC=8$\sqrt{2}$,
∴S△EFO=$\frac{1}{2}$OF•EF=$\frac{1}{2}$(-k)<8$\sqrt{2}$,
∴k>-16$\sqrt{2}$.故①错误;
②∵S菱形OABC=OC•OH=8OH=32$\sqrt{2}$,
∴OH=4$\sqrt{2}$,故②正确;
③在Rt△OHA中,
∵OA=OC=8,OH=4$\sqrt{2}$,
∴AH=4$\sqrt{2}$=OH,
∴tan∠AOH=1,
∴∠AOH=45°,
∴∠AOC=45°.
∵四边形OABC是菱形,
∴∠ABO=∠CBO=$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠AOC=22.5°,故③正确;
④由图可知k<0即-k>0,反比例函数y=-$\frac{k}{x}$在一、三象限,
所以在每个象限y随x的增大而减小,故④错误;
⑤tan∠AOC=tan45°=1,故⑤正确.
故选B.
点评 本题主要考查了反比例函数的性质、反比例函数图象上点的坐标特征、菱形的性质、勾股定理、特殊角的三角函数值等知识,运用菱形的面积公式(菱形的面积等于底乘以高,也等于对角线乘积的一半)是解决本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
| A. | 0.17×106 | B. | 1.7×105 | C. | 1.7×106 | D. | 17×104 |
| A. | 平行 | B. | 相交 | C. | 垂直 | D. | 不能确定 |
(1)根据郎格数的定义可得:
f(6)=1;f($\frac{1}{6}$)=-1;f($\frac{1}{36}$)=-2;
(2)根据郎格数的性质可得:
$①\frac{f({a}^{a})}{f(a)}$=a(a为正数)
②若f(2)=x(x≠0),则f(3)=1-x,f(4)=2x.
(3)若下表中与数a对应的郎格数f(a)有且只有一个是不正确的,请找出错误的郎格数,说明理由并改正.
| a | 1.5 | 3 | 4 | 9 | 16 | 24 |
| f(a) | 2x+y | $\frac{1+2x+y}{2}$ | 1-2x-y | 1+2x+y | 2-4x-2y | -2x-y |