题目内容
4．
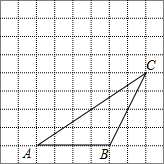如下图，△ABC的顶点都在方格纸的格点上．将△ABC向左平移2格，再向上平移4格．请在图中画出平移后的三角形A′B′C′，再在图中画出三角形A′B′C′的高C′D′、中线A′E．
分析 首先确定A、B、C三点向左平移2格，再向上平移4格的位置，再连接即可得到△A′B′C′．然后再根据网格作C′D′⊥A′B′，垂足为D′，再找出B′C′的中点E，再连接A′E即可．
解答 解：如图所示：
．
点评 此题主要考查了作图--平移变换，作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．
练习册系列答案
相关题目
14．两条直线相交所成的四个角都相等时，这两条直线的位置关系是（ ）
| A． | 平行 | B． | 相交 | C． | 垂直 | D． | 不能确定 |
12．
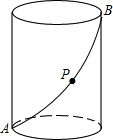如图，圆柱底面半径为4cm，高为8cm，动点P从点A出发，沿着圆柱的侧面移动到点B的最短距离为（ ）
如图，圆柱底面半径为4cm，高为8cm，动点P从点A出发，沿着圆柱的侧面移动到点B的最短距离为（ ）| A． | 2$\sqrt{{π}^{2}+4}$cm | B． | 4$\sqrt{{π}^{2}+4}cm$ | C． | 8$\sqrt{{π}^{2}+4}cm$ | D． | 无法确定 |
19．如果6m=a，那么我们称m为a的郎格数，记为m=f（a）．有上述定义可知：6m=a和m=f（a）中的变量a与m所表示的关系为同一关系，并且有性质：若a、b均为正数，则f（ab）=f（a）+f（b），f（$\frac{a}{b}$）=f（a）-f（b）．
（1）根据郎格数的定义可得：
f（6）=1；f（$\frac{1}{6}$）=-1；f（$\frac{1}{36}$）=-2；
（2）根据郎格数的性质可得：
$①\frac{f（{a}^{a}）}{f（a）}$=a（a为正数）
②若f（2）=x（x≠0），则f（3）=1-x，f（4）=2x．
（3）若下表中与数a对应的郎格数f（a）有且只有一个是不正确的，请找出错误的郎格数，说明理由并改正．
（1）根据郎格数的定义可得：
f（6）=1；f（$\frac{1}{6}$）=-1；f（$\frac{1}{36}$）=-2；
（2）根据郎格数的性质可得：
$①\frac{f（{a}^{a}）}{f（a）}$=a（a为正数）
②若f（2）=x（x≠0），则f（3）=1-x，f（4）=2x．
（3）若下表中与数a对应的郎格数f（a）有且只有一个是不正确的，请找出错误的郎格数，说明理由并改正．
| a | 1.5 | 3 | 4 | 9 | 16 | 24 |
| f（a） | 2x+y | $\frac{1+2x+y}{2}$ | 1-2x-y | 1+2x+y | 2-4x-2y | -2x-y |
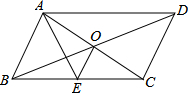如图，?ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=$\frac{1}{2}$BC，连接OE．下列结论：①∠CAD=30°；②S?ABCD=AB•AC；③OB=AB；④∠COD=60°，成立的个数有（ ）