题目内容
8．有大小、形状、颜色、质地完全相同的四张卡片，正面分别写有3、4、5、6四个数字，将这四张卡片背面向上洗匀．（1）从中任意抽取一张，能被3整除的概率是$\frac{1}{2}$．
（2）求从中任意抽取两张，其和恰好是10的概率．
分析 （1）由题意可知3，6能被3整除，所以其概率可求出；
（2）列举出所有情况，看两张卡片和是10的倍数的情况占总情况的多少即可．
解答 解：（1）∵正面分别写有3、4、5、6四个数字，
∴从中任意抽取一张，能被3整除的概率=$\frac{2}{4}=\frac{1}{2}$，
故答案为：$\frac{1}{2}$；
（2）列表得：
| 和 | 3 | 4 | 5 | 6 |
| 3 | 7 | 8 | 9 | |
| 4 | 7 | 9 | 10 | |
| 5 | 8 | 9 | 11 | |
| 6 | 9 | 10 | 11 |
点评 此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
阅读快车系列答案
相关题目
19．如果6m=a，那么我们称m为a的郎格数，记为m=f（a）．有上述定义可知：6m=a和m=f（a）中的变量a与m所表示的关系为同一关系，并且有性质：若a、b均为正数，则f（ab）=f（a）+f（b），f（$\frac{a}{b}$）=f（a）-f（b）．
（1）根据郎格数的定义可得：
f（6）=1；f（$\frac{1}{6}$）=-1；f（$\frac{1}{36}$）=-2；
（2）根据郎格数的性质可得：
$①\frac{f（{a}^{a}）}{f（a）}$=a（a为正数）
②若f（2）=x（x≠0），则f（3）=1-x，f（4）=2x．
（3）若下表中与数a对应的郎格数f（a）有且只有一个是不正确的，请找出错误的郎格数，说明理由并改正．
（1）根据郎格数的定义可得：
f（6）=1；f（$\frac{1}{6}$）=-1；f（$\frac{1}{36}$）=-2；
（2）根据郎格数的性质可得：
$①\frac{f（{a}^{a}）}{f（a）}$=a（a为正数）
②若f（2）=x（x≠0），则f（3）=1-x，f（4）=2x．
（3）若下表中与数a对应的郎格数f（a）有且只有一个是不正确的，请找出错误的郎格数，说明理由并改正．
| a | 1.5 | 3 | 4 | 9 | 16 | 24 |
| f（a） | 2x+y | $\frac{1+2x+y}{2}$ | 1-2x-y | 1+2x+y | 2-4x-2y | -2x-y |
13．
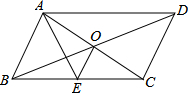如图，?ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=$\frac{1}{2}$BC，连接OE．下列结论：①∠CAD=30°；②S?ABCD=AB•AC；③OB=AB；④∠COD=60°，成立的个数有（ ）
如图，?ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=$\frac{1}{2}$BC，连接OE．下列结论：①∠CAD=30°；②S?ABCD=AB•AC；③OB=AB；④∠COD=60°，成立的个数有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
17．如图，已知△ABC的三条边和三个角六个元素，则下面甲、乙、丙三个三角形中和△ABC全等的图形是（ ）
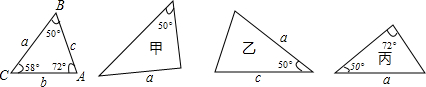
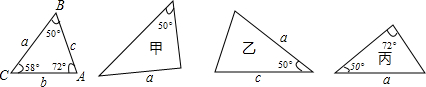
| A． | 只有乙 | B． | 只有丙 | C． | 甲和乙 | D． | 乙和丙 |
