题目内容
10. a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )
a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )| A. | ②⑤ | B. | ②③ | C. | ②③⑤ | D. | ②③④⑤ |
分析 由数轴判断a、b、c的符号和它们绝对值的大小,再判断所给出的式子的符号,写出正确的答案.
解答 解:由数轴知b<0<a<c,|a|<|b|<|c|,
①b+a+(-c)<0,故原式错误;
②(-a)-b+c>0,故正确;
③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1-1+1=1,故正确;
④bc-a<0,故原式错误;
⑤|a-b|-|c+b|+|a-c|=a-b-c-b+c-a=-2b,故正确.
其中正确的有②③⑤.
故选:C.
点评 此题综合考查了数轴、绝对值的有关内容,用几何方法借助数轴来求解,非常直观,且不容易遗漏,体现了数形结合的优点.

练习册系列答案
相关题目
18.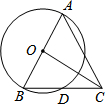 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD至点C,使得DC=BD,连接AC,OC.若AB=5,BD=$\sqrt{5}$,则OC的长为( )
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD至点C,使得DC=BD,连接AC,OC.若AB=5,BD=$\sqrt{5}$,则OC的长为( )
 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD至点C,使得DC=BD,连接AC,OC.若AB=5,BD=$\sqrt{5}$,则OC的长为( )
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD至点C,使得DC=BD,连接AC,OC.若AB=5,BD=$\sqrt{5}$,则OC的长为( )| A. | 4 | B. | $\frac{5}{2}$$\sqrt{3}$ | C. | $\frac{9}{5}$$\sqrt{5}$ | D. | $\frac{\sqrt{65}}{2}$ |
5. 如图,⊙O半径为3,Rt△ABC的顶点A,B在⊙O上,∠A=30°,点C在⊙O内,当点A在圆上运动时,OC的最小值为( )
如图,⊙O半径为3,Rt△ABC的顶点A,B在⊙O上,∠A=30°,点C在⊙O内,当点A在圆上运动时,OC的最小值为( )
 如图,⊙O半径为3,Rt△ABC的顶点A,B在⊙O上,∠A=30°,点C在⊙O内,当点A在圆上运动时,OC的最小值为( )
如图,⊙O半径为3,Rt△ABC的顶点A,B在⊙O上,∠A=30°,点C在⊙O内,当点A在圆上运动时,OC的最小值为( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
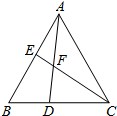 如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F.当点D、E在边BC、AB上运动时,求∠DFC的度数.
如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F.当点D、E在边BC、AB上运动时,求∠DFC的度数.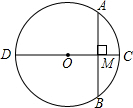 如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5.求AB的长度.
如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5.求AB的长度.