题目内容
1.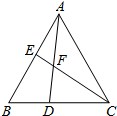 如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F.当点D、E在边BC、AB上运动时,求∠DFC的度数.
如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F.当点D、E在边BC、AB上运动时,求∠DFC的度数.
分析 先依据SAS证明△ABD≌△CAE,则∠BAD=∠ACE,依据三角形的外角的性质可知∠DFC=∠FAC+∠FCA,通过等量代换可得到∠DFC=∠BAC.
解答 解:在△ABD和△CAE中$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠CAE}\\{AE=BD}\end{array}\right.$,
∴△ABD≌△CAE.
∴∠BAD=∠ACE.
∵∠DFC=∠FAC+∠FCA,
∴∠DFC=∠FAC+∠BAD=∠BAC=60°.
点评 本题主要考查的是全等三角形的性质和判定、三角形的外角的性质,依据全等三角形的性质得到∠BAD=∠ACE是解题的关键.

练习册系列答案
相关题目
 如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).
如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).
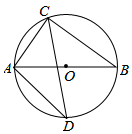 如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB.
如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB. a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )
a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )