题目内容
19.阅读理解:如果a-$\frac{1}{a}$=1,我们可以先将等式两边同时平方得到(a-$\frac{1}{a}$)2=1,再根据完全平方公式计算得:a2-2a•$\frac{1}{a}$+$\frac{1}{{a}^{2}}$=1,即a2-2+$\frac{1}{{a}^{2}}$=1,所以a2+$\frac{1}{{a}^{2}}$=3.请运用上面的方法解决下面问题:如果x2-2x-1=0,则x2+$\frac{1}{{x}^{2}}$的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 把方程两边都除以x得到x-$\frac{1}{x}$=2,再将等式两边同时平方得到(x-$\frac{1}{x}$)2=4,然后根据完全平方公式可计算出x2+$\frac{1}{{x}^{2}}$=6.
解答 解:∵x2-2x-1=0,
∴x-2-$\frac{1}{x}$=0,
即x-$\frac{1}{x}$=2,
(x-$\frac{1}{x}$)2=4,
所以x2+$\frac{1}{{x}^{2}}$-2=4,
即x2+$\frac{1}{{x}^{2}}$=6.
故选C.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.灵活应用完全平方公式是解决问题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目

 a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )
a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )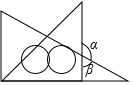 如果我们将一副三角尺按如图所示的位置摆放,并且已知∠a=118°28',那么∠B的度数为61°32'.
如果我们将一副三角尺按如图所示的位置摆放,并且已知∠a=118°28',那么∠B的度数为61°32'.
 如图,△ABC中,∠CAB的平分线与BC的垂直平分线相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.
如图,△ABC中,∠CAB的平分线与BC的垂直平分线相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.