题目内容
2.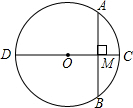 如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5.求AB的长度.
如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5.求AB的长度.
分析 连接OB,首先根据直径的长以及OM:OC=3:5求得OB和OM的长,在直角△OBM中利用勾股定理求得BM的长,然后求得AB的长.
解答  解:连接OB,
解:连接OB,
∵⊙O的直径CD=10,
∴OC=5,
又∵OM:OC=3:5,
∴OM=3,
∵AB⊥CD,且CD为⊙O的直径,
∴△BOM是直角三角形,且AB=2BM;
在Rt△BOM中,OB=5,OM=3,
∴BM=$\sqrt{O{B^2}-O{M^2}}=\sqrt{{5^2}-{3^2}}=4$,
∴AB=2BM=8.
点评 本题主要考查了勾股定理、垂径定理等知识点的应用问题;牢固掌握勾股定理等几何知识点是解题的关键.

练习册系列答案
相关题目
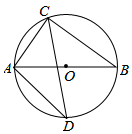 如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB.
如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB. a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )
a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )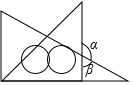 如果我们将一副三角尺按如图所示的位置摆放,并且已知∠a=118°28',那么∠B的度数为61°32'.
如果我们将一副三角尺按如图所示的位置摆放,并且已知∠a=118°28',那么∠B的度数为61°32'.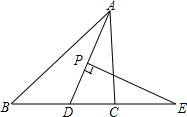 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E