题目内容
6.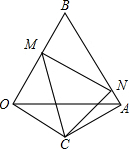 已知,△AOB是等边三角形,△AOC是以AO为底边的等腰三角形,∠AOC=30°,M、N分别是以BO、AB边上的动点,∠MCN=60°,求证:MN=OM+AN.
已知,△AOB是等边三角形,△AOC是以AO为底边的等腰三角形,∠AOC=30°,M、N分别是以BO、AB边上的动点,∠MCN=60°,求证:MN=OM+AN.
分析 利用旋转法将△COM旋转到△CAE的位置,可证△CAE≌△COM,再利用角的相等关系,边的相等关系证明△MCN≌△ECN,利用全等的对应边相等证题.
解答 解:如图,延长BA到E,使AE=OM,连接CE,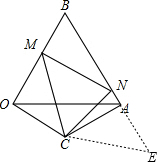
∵△AOB是等边三角形,△AOC是以AO为底边的等腰三角形,∠AOC=30°,
∴∠MOC=∠BOA+∠AOC=60°+30°=90°,∠ACO=180°-∠AOC-∠ACO=120°,
∠CAE=180°-∠BAC=180°-∠BOC=90°,
在△CAE和△COM中,
$\left\{\begin{array}{l}{AE=OM}\\{∠CAE=∠COM}\\{CA=CO}\end{array}\right.$
∴△CAE≌△COM,
∴∠ECA=∠MCO,CE=CM,
∠NCE=∠NCA+∠ECA=∠NCA+∠MCO=∠ACO-∠MCN=120°-60°=60°,
∵在△MCN和△ECN中,
$\left\{\begin{array}{l}{MC=EC}\\{∠MCN=∠ECN}\\{CN=CN}\end{array}\right.$,
∴△MCN≌△ECN,
∴MN=NE,
∴MN=NE=AE+AN=OM+AN.
点评 此题主要考查等腰三角形的性质,全等三角形的判定与性质及等边三角形的性质的综合运用,解决本题的关键是作出辅助线,构建全等三角形.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
1.如图(1),在矩形ABCD中,动点P从点B出发,沿着BC、CD、DA运动到点A停止,设点P运动的路程为x,△ABP的面积为y,如果y与x的函数图象如图(2)所示,则△ABC的周长为( )
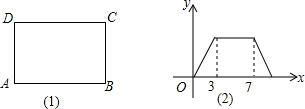

| A. | 9 | B. | 6 | C. | 12 | D. | 7 |
11.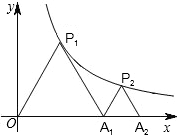 如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
 如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )| A. | -1+$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | -2+2$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
 如图,在平面直角坐标系中,矩形OABC的顶点A.C的坐标分别为(10,0),(0,3),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为(1,3)或(4,3)或(9,3).
如图,在平面直角坐标系中,矩形OABC的顶点A.C的坐标分别为(10,0),(0,3),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为(1,3)或(4,3)或(9,3). 如图,已知?ABCD,AB=$\frac{1}{2}$BC,延长AB至F,使BF=AB,再延长BA至E,使AE=AB,试判断EC与FD的位置关系,并说明其结论正确的理由.
如图,已知?ABCD,AB=$\frac{1}{2}$BC,延长AB至F,使BF=AB,再延长BA至E,使AE=AB,试判断EC与FD的位置关系,并说明其结论正确的理由. 在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm.
在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm.


