题目内容
17. 如图,在平面直角坐标系中,矩形OABC的顶点A.C的坐标分别为(10,0),(0,3),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为(1,3)或(4,3)或(9,3).
如图,在平面直角坐标系中,矩形OABC的顶点A.C的坐标分别为(10,0),(0,3),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为(1,3)或(4,3)或(9,3).
分析 根据当OP=OD时,以及当OD=PD时,分别进行讨论得出P点的坐标.
解答 解: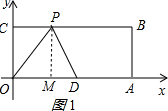 过P作PM⊥OA于M
过P作PM⊥OA于M
(1)当OP=OD时,如图1所示:
OP=5,CO=3,
由勾股定理得:CP=4,
∴P(4,3);
(2)当OD=PD时如图2所示: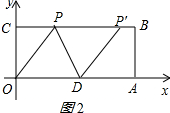
PD=DO=5,PM=3,
由勾股定理得:MD=4,
∴CP=5-4=1或CP'=9,
∴P(1,4)或(9,3);
综上,满足题意的点P的坐标为(1,3)、(4,3)、(9,3),
故答案为:1,3)或(4,3)或(9,3).
点评 此题主要考查了矩形的性质以及坐标与图形的性质和等腰三角形的性质,根据△ODP是腰长为5的等腰三角形进行分类讨论是解决问题的关键.

练习册系列答案
相关题目
8.在平行四边形ABCD中,BC边上的高为AE=4,AB=5,EC=7,则平行四边形ABCD的周长等于( )
| A. | 18 | B. | 30 | C. | 18或30 | D. | 16或40 |
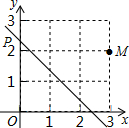 如图,点M的坐标为(3,2),动点P从点O出发,沿y轴以每秒1个单位的速度向上移动,且过点P的直线l:y=-x+b也随之移动,若点M关于l的对称点落在坐标轴上,设点P的移动时间为t,则t的值是2或3.
如图,点M的坐标为(3,2),动点P从点O出发,沿y轴以每秒1个单位的速度向上移动,且过点P的直线l:y=-x+b也随之移动,若点M关于l的对称点落在坐标轴上,设点P的移动时间为t,则t的值是2或3.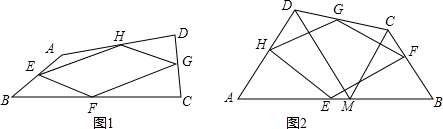
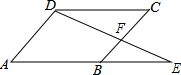 如图,E是?ABCD边AB延长线上的一点,AE=4BE,连接DE交BC于F,则$\frac{BF}{FC}$=$\frac{1}{3}$.
如图,E是?ABCD边AB延长线上的一点,AE=4BE,连接DE交BC于F,则$\frac{BF}{FC}$=$\frac{1}{3}$. 如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的( )
如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的( ) 已知等腰△ABC的底边BC=8,腰长AB=5,现将△ABC按如图所示的方式放在平面直角坐标系中,其中点B与原点重合,点C在x轴上,此时,点A正好落在双曲线l1上.
已知等腰△ABC的底边BC=8,腰长AB=5,现将△ABC按如图所示的方式放在平面直角坐标系中,其中点B与原点重合,点C在x轴上,此时,点A正好落在双曲线l1上.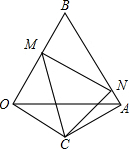 已知,△AOB是等边三角形,△AOC是以AO为底边的等腰三角形,∠AOC=30°,M、N分别是以BO、AB边上的动点,∠MCN=60°,求证:MN=OM+AN.
已知,△AOB是等边三角形,△AOC是以AO为底边的等腰三角形,∠AOC=30°,M、N分别是以BO、AB边上的动点,∠MCN=60°,求证:MN=OM+AN. 如图,平行四边形ABCD,AD=5,AB=6,点A的坐标为(-3,0),则点C的坐标为(6,4).
如图,平行四边形ABCD,AD=5,AB=6,点A的坐标为(-3,0),则点C的坐标为(6,4).