题目内容
9.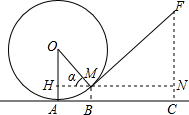 如图,圆形铁环向前滚动时,铁环钩MF保持与铁环相切,已知铁环的半径为20厘米,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=$\frac{3}{5}$.
如图,圆形铁环向前滚动时,铁环钩MF保持与铁环相切,已知铁环的半径为20厘米,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=$\frac{3}{5}$.(1)求点M离地面AC的高度BM(单位:厘米);
(2)设人站立点C与点A的水平距离AC等于52厘米,求铁环钩MF的长度.
分析 (1)过M作AC平行的直线,与OA,FC分别相交于H,N,根据已知条件求出HM,从而得出OH和MB,即可得出点M离地面AC的高度BM;
(2))根据∠MOH+∠OMH=∠OMH+∠FMN,得出FN=$\frac{3}{5}$FM,在Rt△FMN中,根据勾股定理FM,从而得出答案.
解答 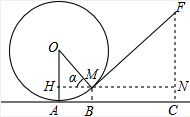 解:(1)过M作AC平行的直线,与OA,FC分别相交于H,N.
解:(1)过M作AC平行的直线,与OA,FC分别相交于H,N.
在Rt△OHM中,
∵∠OHM=90°,OM=20,
∴HM=OM×sinα=12,
∴OH=16,MB=HA=20-16=4(cm),
∴铁环钩离地面的高度为4cm.
(2)∵∠MOH+∠OMH=∠OMH+∠FMN=90°,
∠FMN=∠MOH=α,
∴$\frac{FN}{FM}$=sinα=$\frac{3}{5}$,即得FN=$\frac{3}{5}$FM.
在Rt△FMN中,∠FNM=90°,
MN=BC=AC-AB=52-15=40(cm),
由勾股定理FM2=FN2+MN2,即FM2=($\frac{3}{5}$FM)2+402,
解得FM=50(cm),
则铁环钩的长度FM为50cm.
点评 此题考查了解直角三角形,用到的知识点是勾股定理、特殊角的三角函数值,关键是根据题意作出辅助线,构造直角三角形.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
4.国家统计局初步测算,2011年中国国内生产总值(GDP)471564亿元,比上年增长9.2%.其中471564亿用科学记数法表示记为(保留3个有效数字)( )
| A. | 4.71×1013 | B. | 4.72×1013 | C. | 4.71×1012 | D. | 0.472×1014 |
14.计算$\frac{x-2}{2}$$÷(1-\frac{2}{x})$,所得的正确结果是( )
| A. | $\frac{1}{2}$x | B. | -$\frac{1}{x}$ | C. | $\frac{1}{x}$ | D. | -$\frac{x-2}{x}$ |
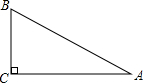 如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.
如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.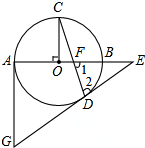 如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上找点E,连接ED,使得∠1=∠2,过点A作⊙O的切线与ED的延长线相交于点G
如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上找点E,连接ED,使得∠1=∠2,过点A作⊙O的切线与ED的延长线相交于点G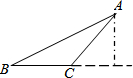 如图,△ABC中,∠B=30°,∠A=15°,若BC边上的高为2,则BC=2$\sqrt{3}$-2.
如图,△ABC中,∠B=30°,∠A=15°,若BC边上的高为2,则BC=2$\sqrt{3}$-2.