题目内容
1.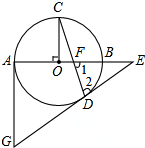 如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上找点E,连接ED,使得∠1=∠2,过点A作⊙O的切线与ED的延长线相交于点G
如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上找点E,连接ED,使得∠1=∠2,过点A作⊙O的切线与ED的延长线相交于点G(1)求证:ED是⊙O的切线;
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
分析 (1)连接OD,证得∠ODE=90°,即可证得结论;
(2)根据切割线定理和勾股定理即可求得AG的长.
解答  (1)证明:连接OD,
(1)证明:连接OD,
∵OC⊥AB,
∴∠OCF+∠OFC=90°,
∵∠1=∠OFC,
∴∠1+∠OCF=90°,
∵OC=OD,
∴∠OCF=∠ODF,
∵∠1=∠2,
∴∠2+∠ODF=90°,
即∠ODE=90°,
∴ED是⊙O的切线;
(2)∵OF:OB=1:3,⊙O的半径为3,
∴OF=1,BF=2,
∴EF=2+BE,
∵∠1=∠2,
∴DE=EF,
∴DF=2+BE,
∵DE是⊙O的切线,
∴DE2=BE•AE,
∴(2+BE)2=BE•(6+BE),
解得BE=2,
∴AE=6+2=8,DE=EF=2+2=4,
∵GA、ED是⊙O的切线,
∴GA=GD,
设AG=x,则GE=x+4,
在RT△AGE中,AG2+AE2=GE2,
∴x2+82=(x+4)2,
解得x=6,
∴AG=6.
点评 本题考查了切线的判定和性质,等腰三角形的判定和性质,勾股定理的应用等,熟练掌握性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.若x1、x2是一元二次方程2x2+4x-3=0的两个根,则x1x2=( )
| A. | -4 | B. | -2 | C. | -3 | D. | -$\frac{3}{2}$ |
12.二次函数y=ax2+2x+3与x轴有2个交点,则a的取值范围是( )
| A. | $a≤\frac{1}{3}$ | B. | $a≥\frac{1}{3}$ | C. | $a>\frac{1}{3}$ | D. | $a<\frac{1}{3}$且a≠0 |
13.已知方程x2+bx+a=0的一个根是a(a≠0),则代数式a+b的值是( )
| A. | -1 | B. | 1 | C. | 0 | D. | 以上答案都不是 |
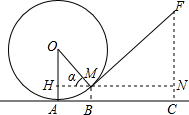 如图,圆形铁环向前滚动时,铁环钩MF保持与铁环相切,已知铁环的半径为20厘米,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=$\frac{3}{5}$.
如图,圆形铁环向前滚动时,铁环钩MF保持与铁环相切,已知铁环的半径为20厘米,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=$\frac{3}{5}$. 如图,每个小正方形的边长都是单位1.
如图,每个小正方形的边长都是单位1.


