��Ŀ����
3����ͼ1���ԡ�ABC��D��BC����һ�㣬����AD����$\frac{A{B}^{2}}{A{C}^{2}}$=$\frac{BD}{CD}$ʱ����ADΪBC���ϵġ�ƽ�����ߡ���ͬ��AB��AC����Ҳ�������Ƶġ�ƽ�����ߡ�����1����ͼ2����ABC�У���BAC=RT�ϣ�AD��BC��D��
֤����ADΪBC���ϵġ�ƽ�����ߡ���
��2����ͼ3����ƽ��ֱ������ϵ�У�B��-4��0����C��1��0������y�������������һ��A��ʹOA�ǡ�ABC��BC���ϵġ�ƽ�����ߡ���
�������A�����ꣻ
����ͼ4����M��$\frac{8}{3}$��0��ΪԲ�ģ�MAΪ�뾶��Բ���ڡ�M����ȡһ��P����x�ύ����⣩������PB��PC��PO����֤��POʼ���ǡ�PBC��BC���ϵġ�ƽ�����ߡ���

���� ��1�����ݻ����жϳ���BAD=��C���õ���BAD�ס�BCA�õ�AB2=BD��BC���ɣ�
��2���������A���꣬���ݡ�ƽ�����ߡ��������̼��ɣ������жϳ���MPC�ס�MBP�õ�����ʽ�����ɣ�
��� �⣺��1���ߡ�BAC=RT�ϣ�
���B+��C=90�㣬
��AD��BC��
���B+��BAD=90�㣬
���BAD=��C��
�ߡ�BDA=��BAC=90�㣬
���BAD�ס�BCA��
��$\frac{AB}{BC}=\frac{BD}{AB}$��
��AB2=BD��BC��
ͬ���ɵã�AC2=CD��BC��
��$\frac{A{B}^{2}}{A{C}^{2}}=\frac{BD}{CD}$��
��ADΪBC���ϵġ�ƽ�����ߡ���
��2������A��0��m����m��0����
��OA=m����OB=4��OC=1��
����AB2=m2+16��AC2=m2+1��
��OAΪBC���ϵġ�ƽ�����ߡ���
��$\frac{A{B}^{2}}{A{C}^{2}}=\frac{BO}{CO}$��
��$\frac{{m}^{2}+16}{{m}^{2}+1}=4$��
��ã�m=2
��A��0��2����
��֤��������PM����ͼ4��
��PM=AM=$\sqrt{��{\frac{8}{3}��}^{2}+4}$=$\frac{10}{3}$��
��MC��MB=$\frac{5}{3}$��$\frac{20}{3}$=$\frac{100}{9}$=PM2��
��$\frac{PM}{MC}=\frac{MB}{PM}$��
�ߡ�PMC=��PMB��
���MPC�ס�MBP��
��$\frac{PC}{BP}=\frac{MC}{PM}$=$\frac{1}{2}$
��$\frac{P{C}^{2}}{B{P}^{2}}=\frac{1}{4}=\frac{OC}{OB}$
��POʼ����BC���ϵġ�ƽ�����ߡ���
���� ������Բ���ۺ��⣬��Ҫ������ֱ�������ε����ʣ����������ε��Ժ��ж������ɶ������¶��壬�Ȿ��Ĺؼ��������¶��塰ƽ�����ߡ���

 �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�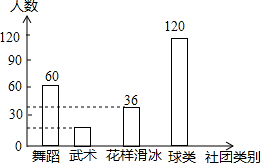 ijУ��չ���Ż��������赸�����������ࣨ��������ƹ������ë�����������������ţ�Ϊ�˽���Уѧ������4�����Ż��ϲ�������ѧУ�����ȡ����ѧ�������ˡ�����ϲ�������š����飬����������ݻ������µ�ͳ��ͼ���������ͼ���е���Ϣ����������⣺
ijУ��չ���Ż��������赸�����������ࣨ��������ƹ������ë�����������������ţ�Ϊ�˽���Уѧ������4�����Ż��ϲ�������ѧУ�����ȡ����ѧ�������ˡ�����ϲ�������š����飬����������ݻ������µ�ͳ��ͼ���������ͼ���е���Ϣ����������⣺������ϲ�������š�����ͳ��ͼ��
| ������� | ���� | ռ�������ı��� |
| �赸 | 60 | 25% |
| ���� | m | 10% |
| �������� | 36 | n% |
| ���� | 120 | 50% |
��2��������ϲ�������ѧ������12����ϲ��ƹ��������У��2600��ѧ�����Թ���ȫУ��ϲ��ƹ�����������
| A�� | $\frac{1}{2}$ | B�� | 2 | C�� | $\sqrt{3}$ | D�� | ��ȷ�� |
 �����Ķ������ѧ����������Ҫ;����ijУ��ίΪ�˽�ѧ�������Ķ�������������˱�Уn��ѧ����ͳ������ƽ��ÿ������Ķ�ʱ��t��ʱ����������ʱ��t�ij��̷�ΪA��B��C��D���࣬��A��0��t��0.5����B��0.5��t��1����C��1��t��1.5����D��t��1.5�������ݳ���������������ͳ��ͼ��
�����Ķ������ѧ����������Ҫ;����ijУ��ίΪ�˽�ѧ�������Ķ�������������˱�Уn��ѧ����ͳ������ƽ��ÿ������Ķ�ʱ��t��ʱ����������ʱ��t�ij��̷�ΪA��B��C��D���࣬��A��0��t��0.5����B��0.5��t��1����C��1��t��1.5����D��t��1.5�������ݳ���������������ͳ��ͼ��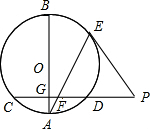 ��ͼ��AB��ԲO��һ��ֱ������CD��ֱ��AB������Ϊ��G��E���ӻ�BD��һ�㣬��E����������CD���ӳ��߽��ڵ�P������AE����CD�ڵ�F��
��ͼ��AB��ԲO��һ��ֱ������CD��ֱ��AB������Ϊ��G��E���ӻ�BD��һ�㣬��E����������CD���ӳ��߽��ڵ�P������AE����CD�ڵ�F�� ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-x-3��������y=x2+mx+n�ཻ��A��B������ͬ�ĵ㣬���е�A��x���ϣ�
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-x-3��������y=x2+mx+n�ཻ��A��B������ͬ�ĵ㣬���е�A��x���ϣ�