题目内容
8. 如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于A、B两个不同的点,其中点A在x轴上.
如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于A、B两个不同的点,其中点A在x轴上.(1)n=3m-9(用含m的代数式表示);
(2)若点B为该抛物线的顶点,求m、n的值;
(3)①设m=-2,当-3≤x≤0时,求二次函数y=x2+mx+n的最小值;
②若-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4,求m的值.
分析 (1)求出点A坐标(-3,0)代入抛物线解析式即可.
(2)利用配方法求出顶点坐标,代入直线解析式即可.
(3)分三种情形①当-$\frac{m}{2}$≤-3时②当-3<-$\frac{m}{2}$≤0时③当-$\frac{m}{2}$>0时,分别列出方程即可解决.
解答 解:(1)∵点A坐标(-3,0)代入抛物线y=x2+mx+n,得9-3m+n=0,
∴n=3m-9.
故答案为3m-9.
(2)∵抛物线为y=x2+mx+3m-9=(x+$\frac{m}{2}$)2-$\frac{{m}^{2}}{4}$+3m-9,
∴顶点为(-$\frac{m}{2}$,-$\frac{{m}^{2}}{4}$+3m-9),
∴-$\frac{{m}^{2}}{4}$+3m-9=$\frac{m}{2}$-3,
整理得m2-10m+24=0,
∴m=4或6.
∴m=4,n=3和m=6,n=9.
(3)∵-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4,y=x2+mx+3m-9=(x+$\frac{m}{2}$)2-$\frac{{m}^{2}}{4}$+3m-9,
①当-$\frac{m}{2}$≤-3时,x=-3时,y=-4,
∴9-3m+3m-9=-4,
无解不合题意.
②当-3<-$\frac{m}{2}$≤0时,x=-$\frac{m}{2}$时,y=-4,
∴-$\frac{{m}^{2}}{4}$+3m-9=-4,
∴m=2或-10(舍弃)
∴m=2.
③当-$\frac{m}{2}$>0时,x=O时,y=-4,
∴3m-9=-4,
∴m=$\frac{5}{3}$不合题意舍弃.
综上所述m=2.
点评 本题考查二次函数的最值、一次函数等知识,解题的关键是掌握待定系数法确定函数解析式,学会构建二次函数,利用二次函数的性质解决问题,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案| A. | 2.15×107 | B. | 0.125×108 | C. | 2.15×108 | D. | 0.125×109 |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 9 | B. | 9$\sqrt{3}$ | C. | 6 | D. | 6$\sqrt{3}$ |
| A. | 6.77×1012 | B. | 67.7×1012 | C. | 6.77×1013 | D. | 67.7×1013 |

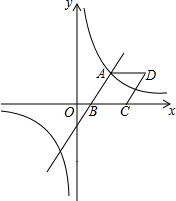 如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.
如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.