题目内容
14.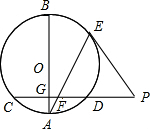 如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.(1)求证:PE=PF
(2)已知AG=4,AF=5,EF=25,求圆O的直径.
分析 (1)如图1,连接OE,根据切线的性质得出∠PEO=90°,求出∠PEF=∠PFE,根据等腰三角形的判定得出即可;
(2)如图2,连接BE,根据相似三角形的判定得出△AGF∽△AEB,得出比例式,代入求出即可.
解答 (1)证明:如图1,连接OE,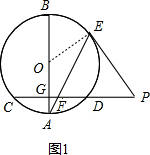
∵EP是⊙O的切线,
∴∠PEO=90°,
∴∠OEA+∠PEF=90°,
∵AB⊥CD,
∴∠AGF=90°,
∴∠A+∠AFG=90°,
∵OE=OA,
∴∠OEA=∠OAE,
∴∠PEF=∠AFG,
∵∠EFP=∠AFG,
∴∠PEF=∠PFE,
∴PE=PF;
(2)解:如图2,连接BE,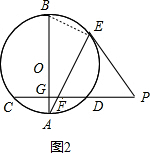
∵AB为直径,
∴∠AEB=90°,
∵∠AGF=90°,
∴∠AGF=∠AEB,
∵∠A=∠A,
∴△AGF∽△AEB,
∴$\frac{AG}{AE}$=$\frac{AF}{AB}$,
∵AG=4,AF=5,EF=25,
∴$\frac{4}{5+25}$=$\frac{5}{AB}$,
∴AB=$\frac{75}{2}$,
即圆O的直径为$\frac{75}{2}$.
点评 本题考查了切线的性质,等腰三角形的性质和判定,相似三角形的性质和判定的应用,能综合运用知识点进行推理和计算是解此题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
19.中央电视台2016年春晚支付宝互动集五福分大奖活动赢得几亿观众的参与,最终全国约79万观众平均分了2.15亿元大奖,把数2.15亿用科学记数法表示为( )
| A. | 2.15×107 | B. | 0.125×108 | C. | 2.15×108 | D. | 0.125×109 |
6.一组数据1,3,2,5,8,7,1的中位数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
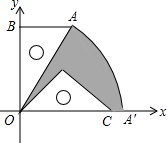 如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π)
如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π)
 如图,点A(2,n)在反比例函数y=$\frac{3}{x}$的图象上,点B在第二象限,∠AOB=90°,∠OBA=30°,在小组合作学习中,四位同学发现并提出了以下四个结论,其中正确的有( )个.
如图,点A(2,n)在反比例函数y=$\frac{3}{x}$的图象上,点B在第二象限,∠AOB=90°,∠OBA=30°,在小组合作学习中,四位同学发现并提出了以下四个结论,其中正确的有( )个.