题目内容
16.若关于x的不等式0≤x2+mx+2≤1中,有且仅有一个x使其成立,求m的值.分析 令y=x2+mx+2,若最小值≤1,则有无数个x的值符合条件,故最小值为1,利用函数的顶点坐标公式即可得出结论.
解答 解:令y=x2+mx+2,
∵关于x的不等式0≤x2+mx+2≤1中,有且仅有一个x使其成立,
∴最小值≤1,则有无数个x的值符合条件,
∴最小值为1,
∴$\frac{8-{m}^{2}}{4}$=1,解得m=±2.
点评 本题考查的是二次函数与不等式组,根据题意利用二次函数的顶点坐标公式求解是解答此题的关键.

练习册系列答案
相关题目
7.已知x=1是方程x2+bx-2=0的一个根,则b的值是( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
 如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象如图所示,则这个二次函数的关系式为y=-$\frac{1}{2}$x2+2x+$\frac{5}{2}$.
如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象如图所示,则这个二次函数的关系式为y=-$\frac{1}{2}$x2+2x+$\frac{5}{2}$. 如图,四边形ABCD中,∠C=∠D=90°,以AB为直径的⊙O交CD于E、F,交BC于G,AD=2,BC=3,CD=7,求DE的长.
如图,四边形ABCD中,∠C=∠D=90°,以AB为直径的⊙O交CD于E、F,交BC于G,AD=2,BC=3,CD=7,求DE的长.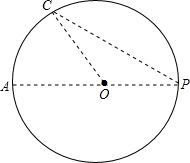 点P到⊙O上的最大距离为10cm.最小距离为5cm.求⊙O的半径.
点P到⊙O上的最大距离为10cm.最小距离为5cm.求⊙O的半径. 在△ABC中点D是BC上一点,∠BAC=90°,∠C=30°,作AC的中垂线DE交BC于D点,连接AD,求证:△ABD是等边三角形.
在△ABC中点D是BC上一点,∠BAC=90°,∠C=30°,作AC的中垂线DE交BC于D点,连接AD,求证:△ABD是等边三角形. 如图,正方形网络中小方格的边长为1,A、B、C都是格点.
如图,正方形网络中小方格的边长为1,A、B、C都是格点.