题目内容
8.在平面直角坐标系xOy中,抛物线的表达式是y=$\frac{1}{4}$x2+1,点C的坐标为(-4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,求出点M的坐标.分析 首先求得OC,利用平行四边形的性质与二次函数的对称性求得A、B点的坐标,确定点M的坐标即可.
解答 解:如图,
∵OABC是平行四边形,
∴AB∥OC,且AB=OC=4,
∵A,B在抛物线上,y轴是抛物线的对称轴,
∴A,B的横坐标分别是2和-2,
代入y=$\frac{1}{4}$x2+1得,A(2,2),B(-2,2),
∴M点的坐标是(0,2).
点评 此题考查二次函数的性质,平行四边形的性质,掌握二次函数的对称性是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 小彬家的墙上钉着一个用彩绳围成的三角形(如图,单位:cm),小彬通过移动钉子,把它变成一个(如图虚线所示)正三角形,则正三角形的边长为7cm.
小彬家的墙上钉着一个用彩绳围成的三角形(如图,单位:cm),小彬通过移动钉子,把它变成一个(如图虚线所示)正三角形,则正三角形的边长为7cm. 等腰梯形ABCD的底角为60°,上底CD长为3cm,下底AB长为5cm,求:
等腰梯形ABCD的底角为60°,上底CD长为3cm,下底AB长为5cm,求: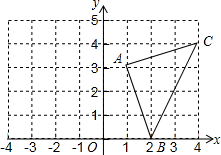 如图,A(1,3),B(2,0),C(4,4).
如图,A(1,3),B(2,0),C(4,4). 如图,在△ABC中,∠BAC的外角平分线的反向延长线与∠ACB的平分线交于点O,则∠O和∠B是什么数量关系?并说明你的理由.
如图,在△ABC中,∠BAC的外角平分线的反向延长线与∠ACB的平分线交于点O,则∠O和∠B是什么数量关系?并说明你的理由. 如图,AD⊥CD,AB=13,BC=12,CD=4,AD=3,∠CAB=α,求∠B.(用α表示)
如图,AD⊥CD,AB=13,BC=12,CD=4,AD=3,∠CAB=α,求∠B.(用α表示)