题目内容
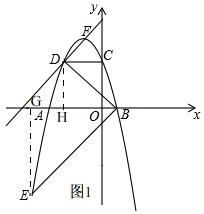
10. 如图,二次函数y=ax2-2amx-3am2(a,m是常数,且m<0)的图象与x轴交于A、B(点A位于点B的左侧),与y轴交于点C(0,3),作CD∥AB交抛物线于点D,连接BD,过点B作射线BE交抛物线于点E,使得AB平分∠DBE.
如图,二次函数y=ax2-2amx-3am2(a,m是常数,且m<0)的图象与x轴交于A、B(点A位于点B的左侧),与y轴交于点C(0,3),作CD∥AB交抛物线于点D,连接BD,过点B作射线BE交抛物线于点E,使得AB平分∠DBE.(1)求点A,B的坐标;(用m表示)
(2)$\frac{BD}{BE}$是否为定值?若是,求出这个定值;若不是,请说明理由.
(3)抛物线y=ax2-2amx-3am2的顶点为F,直线DF上是否存在唯一一点M,使得∠OMA=90°?若存在,求出此时m的值;若不存在,请说明理由.
分析 (1)利用因式分解法即可得出点A,B坐标;
(2)先表示出DH,BH,再利用角平分线判断出△BDH∽△BEG,即可得出结论;
(3)先求出点D,F坐标,进而得出直线DF解析式,求出OP,PN,再取OA的中点,求出MN,OM,由存在唯一一点得出PN和PO都和⊙M相切,即PM是∠OPN的平分线,用角平分线定理即可求出m.
解答 解:(1)由ax2-2amx-3am2=0得,x1=-m,x2=3m,
则B(-m,0),A(3m,0),
(2) $\frac{BD}{BE}$是定值,为$\frac{3}{5}$;
$\frac{BD}{BE}$是定值,为$\frac{3}{5}$;
理由:过点D作DH⊥AB于H,过点E作EG⊥AB于G,
将点C(0,3)代入y=ax2-2amx-3am2得,
a=-$\frac{1}{{m}^{2}}$;
∴y=ax2-2amx-3am2=-$\frac{1}{{m}^{2}}$x2+$\frac{2}{m}$x+3,
∵CD∥AB,
∴点D的坐标为(2m,3),
∴OH=-2m,DH=3,
∴BH=-3m
∵AB平分∠DBE,
∴∠DBH=∠EBG,又∠DHB=∠EGB=90°,
∴△BDH∽△BEG,
∴$\frac{BD}{BE}=\frac{DH}{EG}=\frac{BH}{BG}$,
设E(n,-$\frac{1}{{m}^{2}}$×n2+$\frac{2}{m}$×n+3),
∴OG=-n,EG=$\frac{1}{{m}^{2}}$×n2-$\frac{2}{m}$×n-3,
∴BG=-m-n,
∴$\frac{3}{\frac{1}{{m}^{2}}×{n}^{2}-\frac{2n}{m}-3}=\frac{-3m}{-m-n}$,
∴n=4m,
∴E(4m,5),
∵BH=BO+OH=-m-2m=-3m,BG=BO+OG=-m-4m=-5m,
∴$\frac{BD}{BE}=\frac{BH}{BG}=\frac{-3m}{-5m}=\frac{3}{5}$,
(3)存在,
理由:如图2,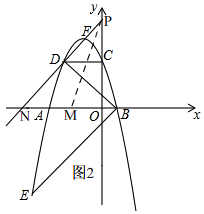 ∵B(-m,0),A(3m,0),
∵B(-m,0),A(3m,0),
∴F(m,4),
∵D(2m,3),
∴直线DF的解析式为y=-$\frac{1}{m}$x+5,
∴N(5m,0),P(0,5),
∴OP=5,PN=$\sqrt{(5m)^{2}+{5}^{2}}$=5$\sqrt{{m}^{2}+1}$
取OA的中点M,
∵A(3m,0),N(5m,0),
∴M($\frac{3}{2}$m.0),
∴OM=-$\frac{3}{2}$m.MN=-$\frac{7}{2}$m,
假设直线DF上是存在唯一一点M,使得∠OMA=90°,
∴以OA为直径的⊙M与PN,PO相切,
∴PM是∠OPN的角平分线,
∴$\frac{PN}{OP}=\frac{MN}{OM}$,
∴$\frac{5\sqrt{{m}^{2}+1}}{5}=\frac{-\frac{7}{2}m}{-\frac{3}{2}m}$,
∴m=$\frac{2\sqrt{10}}{3}$(舍)或m=-$\frac{2\sqrt{10}}{3}$.
点评 此题是二次函数综合题,主要考查了待定系数法,相似三角形的性质和判定,角平分线的性质,作出辅助线是解本题的关键也是难点,此题用到方程的思想解决几何图形问题,是一道典型的题目.

 如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=1,OC=6,试求出正方形ADEF的边长.
如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=1,OC=6,试求出正方形ADEF的边长.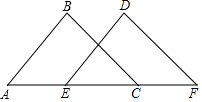 如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.求证:∠B=∠D.
如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.求证:∠B=∠D.
 列方程解应用题:
列方程解应用题: