题目内容
气温随着高度的增加而下降,下降规律是从地面到高空11km处,每升高1km,气温下降6℃,高于11km时,气温几乎不再变化,设地面的气温为38℃,高空中xkm的气温为y℃.求:
(1)当0≤x≤11时,求y与x之间的关系式.
(2)求当x=2、5、8、11时,y的值.
(3)求在离地面13km的高空处,气温是多少度?
(4)当气温是-16℃时,问在离地面多高的地方?
(1)当0≤x≤11时,求y与x之间的关系式.
(2)求当x=2、5、8、11时,y的值.
(3)求在离地面13km的高空处,气温是多少度?
(4)当气温是-16℃时,问在离地面多高的地方?
考点:一次函数的应用
专题:
分析:(1)利用地面的气温减去升高xkm下降的温度即可;
(2)把x=2、5、8、11代入(1)中的代数式求得答案即可;
(3)离地面13km的高空与离地面11km的高空温度相同;
(4)令y=-16,利用(1)中的代数式建立方程求得未知数的值即可.
(2)把x=2、5、8、11代入(1)中的代数式求得答案即可;
(3)离地面13km的高空与离地面11km的高空温度相同;
(4)令y=-16,利用(1)中的代数式建立方程求得未知数的值即可.
解答:解:(1)y=38-6x(0≤x≤11);
(2)当x=2时,y=26;
当x=5时,y=8;
当x=8时,y=-10;
当x=11时,y=-28;
(3)离地面13km的高空处,与离地面11km的高空温度相同是-28℃;
(4)令y=-16,
则38-6x=-16,
解得x=9.
答:离地面9km的地方.
(2)当x=2时,y=26;
当x=5时,y=8;
当x=8时,y=-10;
当x=11时,y=-28;
(3)离地面13km的高空处,与离地面11km的高空温度相同是-28℃;
(4)令y=-16,
则38-6x=-16,
解得x=9.
答:离地面9km的地方.
点评:此题考查一次函数的实际运用,找出基本数量关系,列出解析式是解决问题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,直线l1:y1=kx+b与反比例函数y2=
如图,直线l1:y1=kx+b与反比例函数y2=
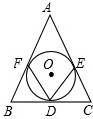 如图,⊙O与△ABC的三边都相切,切点分别为D、E、F,如果∠FDE=70°,那么∠A是多少度?
如图,⊙O与△ABC的三边都相切,切点分别为D、E、F,如果∠FDE=70°,那么∠A是多少度?