题目内容
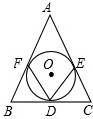如图，⊙O与△ABC的三边都相切，切点分别为D、E、F，如果∠FDE=70°，那么∠A是多少度？考点：三角形的内切圆与内心
专题：
分析：此题可以构造圆周角所对的弧，弧所对的圆心角，进一步根据切线的性质定理以及四边形的内角和求解．
解答：
解：连接IE，IF，
∵⊙O与△ABC的三边都相切，
∴∠AFI=∠AEI=90°，
∴∠A=180°-∠FIE=180°-2∠FDE=40°．
解：连接IE，IF，∵⊙O与△ABC的三边都相切，
∴∠AFI=∠AEI=90°，
∴∠A=180°-∠FIE=180°-2∠FDE=40°．
点评：本题考查了三角形的内切圆与内心，综合运用了圆周角定理以及切线的性质定理和四边形的内角和定理．
练习册系列答案
快捷英语周周练系列答案
相关题目
如果线段AB=3cm，BC=1cm，那么A、C两点的距离d的长度为（ ）
| A、4cm |
| B、2cm |
| C、4cm或2cm |
| D、小于或等于4cm，且大于或等于2cm |
在圆O中，∠ACB=∠BCA=60°，AC=2
如图，在△ABC中，内切圆I和边BC、CA、AB分别相切于点D、E、F，若∠B=60°，∠C=70°，求∠EDF的度数．
将两张宽度都为1的纸条叠放成如图所示的图形，所成四边形的锐角为α，则这个四边形的面积为（ ）A、
| ||
| B、tanα | ||
C、
| ||
D、
|
如图所示，回答各题的方位角：