题目内容
 如图,直线l1:y1=kx+b与反比例函数y2=
如图,直线l1:y1=kx+b与反比例函数y2=| m |
| x |
| m |
| x |
(1)求反比例函数的解析式和c的值.
(2)求△BOC的面积
(3)直接写出当kx+b≥
| m |
| x |
(4)若过原点O的直线交反比列函数于P、Q两点(P在第二象限、Q在第四象限)当以P、A、C、Q为顶点的四边形的面积为30时,求点Q的坐标.
考点:反比例函数综合题
专题:
分析:(1)利用待定系数法可求出m的值,即可求出点B的坐标,把点B代入直线l2即可得出c的值.
(2)联立解出点C,D的坐标,利用S△BOC=S△BOD+S△COD求解即可.
(3)由图象可得,-4≤x≤-1或x>0.
(4)先得出P、A、C、Q为顶点的四边形是平行四边形,设Q(m,-
),由S△COQ分两种情况求解即可.
(2)联立解出点C,D的坐标,利用S△BOC=S△BOD+S△COD求解即可.
(3)由图象可得,-4≤x≤-1或x>0.
(4)先得出P、A、C、Q为顶点的四边形是平行四边形,设Q(m,-
| 4 |
| m |
解答:解:(1)∵A(-1,4)在反比例图象上,
∴m=-1×4=-4,
∴反比例函数的解析式为:y=
,
∴B(-4,1),
把B(-4,1),代入y3=-x+c得1=4+c,
∴c=-3;
(2)∵直线l2与反比例函数,相交于B、C两点,
∴反比例函数与直线l2联立得
,解得
或
,
∴C(1,-4),B(-4,1).
∵直线l2交y轴于点D,
∴y3=-3,
∴D(0,-3).
∵OD=3,△BOD中OD边上的高为|-4|,△COD中OD边上的高为1,
∴S△BOC=S△BOD+S△COD=
×3×4+
×3×1=
,
(3)由图象可得,-4≤x≤-1或x>0时,有kx+b≥
,
(4)如图,
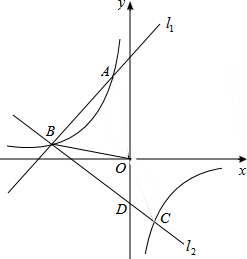
∵A(-1,4)和C(1,-4)关于原点对称,
∴直线AC过原点O,
∴由题意知以P、A、C、Q为顶点的四边形是平行四边形,
∴S△COQ=
×30=
,
设Q(m,-
),
①
(
+4)(m-1)=
,化简得,4m2-15m-4=0,解得m=-
(舍去),m=4.
∴Q(4,-1),
②
(
+4)(1-m)=
,化简得,4m2+15m-4=0,解得m=
(舍去),m=-4.
∴Q(
,-16),
综上所述,点Q的坐标为(4,-1)或(
,-16).
∴m=-1×4=-4,
∴反比例函数的解析式为:y=
| -4 |
| x |
∴B(-4,1),
把B(-4,1),代入y3=-x+c得1=4+c,
∴c=-3;
(2)∵直线l2与反比例函数,相交于B、C两点,
∴反比例函数与直线l2联立得
|
|
|
∴C(1,-4),B(-4,1).
∵直线l2交y轴于点D,
∴y3=-3,
∴D(0,-3).
∵OD=3,△BOD中OD边上的高为|-4|,△COD中OD边上的高为1,
∴S△BOC=S△BOD+S△COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
(3)由图象可得,-4≤x≤-1或x>0时,有kx+b≥
| m |
| x |
(4)如图,

∵A(-1,4)和C(1,-4)关于原点对称,
∴直线AC过原点O,
∴由题意知以P、A、C、Q为顶点的四边形是平行四边形,
∴S△COQ=
| 1 |
| 4 |
| 15 |
| 2 |
设Q(m,-
| 4 |
| m |
①
| 1 |
| 2 |
| 4 |
| m |
| 15 |
| 2 |
| 1 |
| 4 |
∴Q(4,-1),
②
| 1 |
| 2 |
| 4 |
| m |
| 15 |
| 2 |
| 1 |
| 4 |
∴Q(
| 1 |
| 4 |
综上所述,点Q的坐标为(4,-1)或(
| 1 |
| 4 |
点评:本题主要考查了反比例函数的综合题,解题的关键是利用图象获取有用的信息.

练习册系列答案
相关题目
如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )
| A、4cm |
| B、2cm |
| C、4cm或2cm |
| D、小于或等于4cm,且大于或等于2cm |

 如图,在正方形ABCD中,取AD,CD的边的中点E,F,连接CE,BF交于点G,连接AG,试判断AG与AB是否相等,并说明理由.
如图,在正方形ABCD中,取AD,CD的边的中点E,F,连接CE,BF交于点G,连接AG,试判断AG与AB是否相等,并说明理由.