题目内容
同一个圆的中内接正方形与其外切正方形的周长比是 ,面积比是 .
考点:正多边形和圆
专题:
分析:如图,设OB=x,即可得出AB、CD的长,从而得出圆内接正方形与其外切正方形的边长,再由相似多边形的性质得出周长之比和面积之比.
解答: 解:设OB=x,
解:设OB=x,
∴AB=x,
∴由勾股定理得OA=
x,
∴OD=CD=
x,
∴OC=2x,
∴圆内接正方形与其外切正方形的周长之比=x:
x=1:
,
∴圆内接正方形与其外切正方形的面积之比=(1:
)2=1:2,
故答案为1:
,1:2.
 解:设OB=x,
解:设OB=x,∴AB=x,
∴由勾股定理得OA=
| 2 |
∴OD=CD=
| 2 |
∴OC=2x,
∴圆内接正方形与其外切正方形的周长之比=x:
| 2 |
| 2 |
∴圆内接正方形与其外切正方形的面积之比=(1:
| 2 |
故答案为1:
| 2 |
点评:本题考查了正多边形和圆,求得圆内接正方形与其外切正方形的边长之比是解题的关键.

练习册系列答案
相关题目
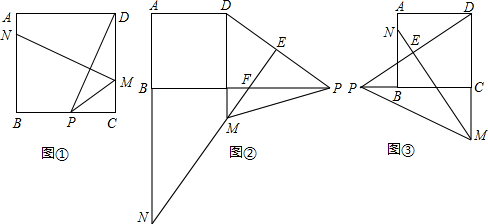
 如图,在正方形ABCD中,取AD,CD的边的中点E,F,连接CE,BF交于点G,连接AG,试判断AG与AB是否相等,并说明理由.
如图,在正方形ABCD中,取AD,CD的边的中点E,F,连接CE,BF交于点G,连接AG,试判断AG与AB是否相等,并说明理由.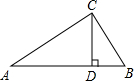 如图,∠ACB=90°,CD⊥AB于D.则:
如图,∠ACB=90°,CD⊥AB于D.则: 在圆O中,∠ACB=∠BCA=60°,AC=2
在圆O中,∠ACB=∠BCA=60°,AC=2