题目内容
直线上有两点A,B,再在该直线上取点C,使BC=
AB,D是AC的中点,若BD=6cm,求线段AB的长.
| 1 |
| 2 |
考点:两点间的距离
专题:
分析:由于点C的位置不能确定,故应分点C在在AB之间与点C在AB外两种情况进行讨论.
解答: 解:如图1所示,
解:如图1所示,
∵BC=
AB,D是AC的中点,
∴设CD=x,则BC=2x,
∴BD=CD+BC=x+2x=3x=6cm,解得x=2cm,
∴AB=AC+BC=2x+2x=4x=8cm;
如图2所示,
设BC=x,
∵BC=
AB,
∴AB=2x,
∴AC=AB+BC=2x+x=3x.
∵D是AC的中点,
∴DC=
AC=
x,
∵BD=6cm,
∴BD=DC-BC=
x-x=6cm,
∴x=12cm,
∴AB=2x=24cm.
综上所述,线段AB的长为8cm或24cm.
 解:如图1所示,
解:如图1所示,∵BC=
| 1 |
| 2 |
∴设CD=x,则BC=2x,
∴BD=CD+BC=x+2x=3x=6cm,解得x=2cm,
∴AB=AC+BC=2x+2x=4x=8cm;
如图2所示,
设BC=x,
∵BC=
| 1 |
| 2 |
∴AB=2x,
∴AC=AB+BC=2x+x=3x.
∵D是AC的中点,
∴DC=
| 1 |
| 2 |
| 3 |
| 2 |
∵BD=6cm,
∴BD=DC-BC=
| 3 |
| 2 |
∴x=12cm,
∴AB=2x=24cm.
综上所述,线段AB的长为8cm或24cm.
点评:本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )
| A、4cm |
| B、2cm |
| C、4cm或2cm |
| D、小于或等于4cm,且大于或等于2cm |
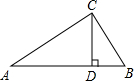 如图,∠ACB=90°,CD⊥AB于D.则:
如图,∠ACB=90°,CD⊥AB于D.则:
 在圆O中,∠ACB=∠BCA=60°,AC=2
在圆O中,∠ACB=∠BCA=60°,AC=2 如图所示,回答各题的方位角:
如图所示,回答各题的方位角: