题目内容
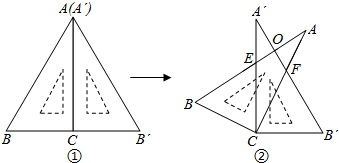
13.谢尔宾斯基地毯,最早是由波兰数学家谢尔宾斯基制作出来的:把一个正三角形分成全等的4个小正三角形,挖去中间的一个小三角形;对剩下的3个小正三角形再分别重复以上做法…将这种做法继续进行下去,就得到小格子越来越多的谢尔宾斯基地毯(如图).若图1中的阴影三角形面积为1,则图5中的所有阴影三角形的面积之和是$\frac{81}{256}$.
分析 根据题意,每次挖去等边三角形的面积的$\frac{1}{4}$,剩下的阴影部分面积等于原阴影部分面积的$\frac{3}{4}$,然后根据有理数的乘方列式计算即可得解.
解答 解:图2阴影部分面积=1-$\frac{1}{4}$=$\frac{3}{4}$,
图3阴影部分面积=$\frac{3}{4}$×$\frac{3}{4}$=($\frac{3}{4}$)2,
图4阴影部分面积=$\frac{3}{4}$×($\frac{3}{4}$)2=($\frac{3}{4}$)3,
图5阴影部分面积=$\frac{3}{4}$×($\frac{3}{4}$)3=($\frac{3}{4}$)4=$\frac{81}{256}$.
故答案为:$\frac{81}{256}$.
点评 本题是对图形变化规律的考查,观察出每次挖出后剩下的阴影部分面积等于原阴影部分面积的$\frac{3}{4}$是解题的关键.

练习册系列答案
相关题目
5.若平行四边形的对角线长度分别为6和8,一边长为2x-1,则x的取值范围为( )
| A. | 0<x<4 | B. | 1<x<4 | C. | 0<x<3 | D. | 1<x<3 |
2.在四边形ABCD中,若∠A与∠C之和等于四边形外角和的一半,∠B比∠D大15°,则∠B的度数等于( )
| A. | 150° | B. | 97.5° | C. | 82.5° | D. | 67.5° |
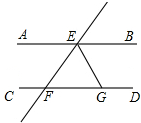 已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠EFD=72°,则∠EGC等于多少度?
已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠EFD=72°,则∠EGC等于多少度?
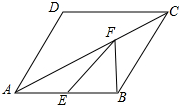 如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.
如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.