题目内容
2.在四边形ABCD中,若∠A与∠C之和等于四边形外角和的一半,∠B比∠D大15°,则∠B的度数等于( )| A. | 150° | B. | 97.5° | C. | 82.5° | D. | 67.5° |
分析 根据∠A与∠C之和等于四边形外角和的一半,四边形的外角和为360°,得到∠A+∠C=180°,根据四边形的内角和为360°∠B+∠D=360°-(∠A+∠C)=180°①,根据∠B比∠D大15°,得到∠B-∠D=15°②,所以①+②得:2∠B=195°,所以∠B=97.5°
解答 解:∵∠A与∠C之和等于四边形外角和的一半,四边形的外角和为360°,
∴∠A+∠C=180°,
∴∠B+∠D=360°-(∠A+∠C)=180°①,
∵∠B比∠D大15°,
∴∠B-∠D=15°②,
①+②得:2∠B=195°,
∴∠B=97.5°.
故选:B.
点评 本题考查了多边形的内角与外角,解决本题的关键是熟记四边形的内角和与外角和.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
10.用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )
| A. | 有一个内角小于90° | B. | 有一个内角小于或等于90° | ||
| C. | 每一个内角都小于90° | D. | 每一个内角都大于90° |
7.在一个直角三角形中,若其中两边长分别为5cm,3cm,则第三边长为( )
| A. | 4cm | B. | 4cm或$\sqrt{34}$cm | C. | $\sqrt{34}$cm | D. | 不存在 |
14.从图1到图2的变化过程可以发现的代数结论是( )
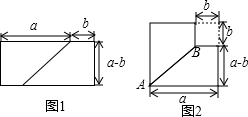

| A. | (a+b)(a-b)=a2-b2 | B. | a2-b2=(a+b)(a-b) | C. | (a+b)2=a2+2ab+b2 | D. | a2+2ab+b2=(a+b)2 |
12.如果x2+kxy+9y2是一个完全平方式,那么k的值为( )
| A. | 6 | B. | -6 | C. | ±6 | D. | 18 |
 如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.
如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.