题目内容
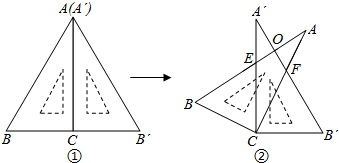
3.将两块大小相同的含30°角的直角三角板(∠BAC=∠B′A′C=30°)按图①方式放置,固定三角板A′B′C,然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置,AB与A′C交于点E,AC与A′B′交于点F,AB与A′B′相交于点O.(1)当旋转角为30度时,CF=CB′;
(2)在上述条件下,AB与A′B′垂直吗?请说明理由.
分析 (1)由CF=CB′可知∠CFB′=∠CB′F=60°,从而可求得∠FCB′的度数,然后可求得∠A′CA=30°;
(2)由∠A′CA=30°,可求得∠ECB=60°,然后可求得∠A′EO=∠BEC=60°,从而可求得∠A′OE=90°.
解答 解:(1)∵CF=CB′,
∴∠CFB′=∠CB′F=60°.
∴∠A′CA=90°-∠FCB′=90°-60°=30°.
故旋转角为30°时,CF=CB′;
故答案为:30°.
(2)∵∠A′CA=30°,
∴∠BCE=∠ACB-∠A′CA=90°-30°=60°.
∴∠B=∠BCE=∠BEC=60°.
∴∠A′EO=60°.
∴∠A′EO+∠A′=60°+30°=90°.
∴∠A′OE=90°.
∴AB⊥A′B′.
点评 本题主要考查的是旋转的性质和等边三角形的性质和判定,判定出△BCE和△B′CF为等边三角形是解题的关键.

练习册系列答案
相关题目
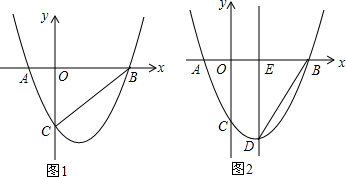
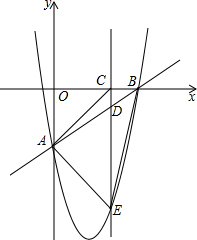 如图,在平面直角坐标系xOy中,直线y=x+m与坐标轴y轴交于点A,与x轴交于点B,过A,B两点的抛物线y=x2+nx-8,点D为线段AB上一动点,过点D作CD垂直x轴于点C,交抛物线于点E.
如图,在平面直角坐标系xOy中,直线y=x+m与坐标轴y轴交于点A,与x轴交于点B,过A,B两点的抛物线y=x2+nx-8,点D为线段AB上一动点,过点D作CD垂直x轴于点C,交抛物线于点E. 如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.
如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.