题目内容
3.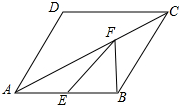 如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.
如图,已知:在?ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.(1)?ABCD的周长是8;
(2)EF+BF的最小值为$\sqrt{3}$.
分析 (1)证明四边ABCD为菱形,从而可求得四边形ABCD的周长;
(2)首先菱形的性质可知点B与点D关于AC对称,从而可知BF=DF,则EF+BF=EF+DF,当点D、F、E共线时,EF+BF有最小值.
解答 解:(1)∵四边形ABCD为平行四边形,
∴AB=CD,AD=BC.
∵AB=AD,
∴AB=CD=AD=BC.
∴?ABCD的周长=2×4=8.
(2)∵AB=CD=AD=BC,
∴四边形ABCD为菱形.
∴点D与点B关于AC对称.
∴BF=DF.
连接DE.
∵E是AB的中点,
∴AE=1.
∴$\frac{AE}{AD}=\frac{1}{2}$
又∵∠DAB=60°,
∴cos∠DAE=$\frac{1}{2}$.
∴△ADE为直角三角形.
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}=\sqrt{{2}^{2}-{1}^{2}}$$\sqrt{3}$.
故答案为:1)8;(2)$\sqrt{3}$.
点评 本题主要考查的是最短路径、平行四边形的性质以及菱形的性质和判定,由轴对称图形的性质将EF+FB的最小值转化为DF+EF的最小值是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
14.从图1到图2的变化过程可以发现的代数结论是( )
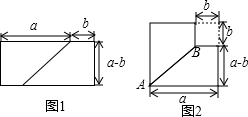

| A. | (a+b)(a-b)=a2-b2 | B. | a2-b2=(a+b)(a-b) | C. | (a+b)2=a2+2ab+b2 | D. | a2+2ab+b2=(a+b)2 |
12.如果x2+kxy+9y2是一个完全平方式,那么k的值为( )
| A. | 6 | B. | -6 | C. | ±6 | D. | 18 |

 如图,已知△ABC中,CD⊥AB于点D,若AB=5,BC=4,∠BCD=30°,求AC的长.
如图,已知△ABC中,CD⊥AB于点D,若AB=5,BC=4,∠BCD=30°,求AC的长. 如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论: