题目内容
1.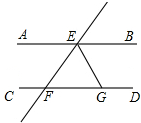 已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠EFD=72°,则∠EGC等于多少度?
已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠EFD=72°,则∠EGC等于多少度?
分析 根据两直线平行,同旁内角互补求出∠BEF,再根据角平分线的定义可得∠BEG=$\frac{1}{2}$∠BEF,然后根据两直线平行,内错角相等即可得解.
解答 解:∵AB∥CD,
∴∠BEF=180°-∠EFD=180°-72°=108°,
∵EG平分∠BEF,
∴∠BEG=$\frac{1}{2}$∠BEF=$\frac{1}{2}$×108°=54°,
∵AB∥CD,
∴∠EGC=∠BEG=54°.
点评 本题主要考查了平行线的性质和角平分线的性质,正确运用两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等是解答此题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
9.已知x+y=8,xy=5,则x2+y2的值是( )
| A. | 84 | B. | 74 | C. | 64 | D. | 54 |
16.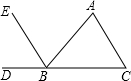 如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
 如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
如图,若∠A=75°,则要使EB∥AC可添加的条件是( )| A. | ∠C=75° | B. | ∠DBE=75° | C. | ∠ABE=75° | D. | ∠EBC=105° |
6.若x<0,则化简$\sqrt{{-x}^{3}y}$的结果是( )
| A. | -x$\sqrt{xy}$ | B. | x$\sqrt{-xy}$ | C. | -x$\sqrt{-xy}$ | D. | x$\sqrt{xy}$ |
10.用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )
| A. | 有一个内角小于90° | B. | 有一个内角小于或等于90° | ||
| C. | 每一个内角都小于90° | D. | 每一个内角都大于90° |
 如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.
如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.