题目内容
4.先化简,再求值:$\frac{{x}^{2}+2x+1}{2x-6}$÷(x-$\frac{1-3x}{x-3}$),其中x为数据0,-1,-3,1,2的平均值.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则计算,约分得到最简结果,求出数据的平均数得到x的值,代入计算即可求出值.
解答 解:原式=$\frac{(x+1)^{2}}{2(x-3)}$÷$\frac{{x}^{2}-3x-1+3x}{x-3}$=$\frac{(x+1)^{2}}{2(x-3)}$•$\frac{x-3}{(x+1)(x-1)}$=$\frac{x+1}{2(x-1)}$,
数据0,-1,-3,1,2的平均值为x=$\frac{1}{5}$×(0-1-3+1+2)=-$\frac{1}{5}$,
则原式=$\frac{-\frac{1}{5}+1}{2(-\frac{1}{5}-1)}$=-$\frac{1}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.下列调查:
①企业招聘,对招聘人员进行面试;
②调查全班同学的身高;
③调查市场上某种食品的色素含量是否符合国家标准;
④调查一批灯泡的使用寿命;
其中符合用全面调查的是( )
①企业招聘,对招聘人员进行面试;
②调查全班同学的身高;
③调查市场上某种食品的色素含量是否符合国家标准;
④调查一批灯泡的使用寿命;
其中符合用全面调查的是( )
| A. | ①② | B. | ①③ | C. | ②④ | D. | ②③ |
9.已知x+y=8,xy=5,则x2+y2的值是( )
| A. | 84 | B. | 74 | C. | 64 | D. | 54 |
16.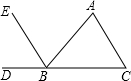 如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
 如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
如图,若∠A=75°,则要使EB∥AC可添加的条件是( )| A. | ∠C=75° | B. | ∠DBE=75° | C. | ∠ABE=75° | D. | ∠EBC=105° |
14.从图1到图2的变化过程可以发现的代数结论是( )
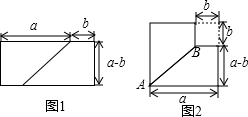

| A. | (a+b)(a-b)=a2-b2 | B. | a2-b2=(a+b)(a-b) | C. | (a+b)2=a2+2ab+b2 | D. | a2+2ab+b2=(a+b)2 |
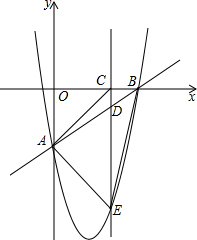 如图,在平面直角坐标系xOy中,直线y=x+m与坐标轴y轴交于点A,与x轴交于点B,过A,B两点的抛物线y=x2+nx-8,点D为线段AB上一动点,过点D作CD垂直x轴于点C,交抛物线于点E.
如图,在平面直角坐标系xOy中,直线y=x+m与坐标轴y轴交于点A,与x轴交于点B,过A,B两点的抛物线y=x2+nx-8,点D为线段AB上一动点,过点D作CD垂直x轴于点C,交抛物线于点E. 如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.
如图,∠AOB=30°,M,Q在OA上,P、N在OB上,OM=1,ON=3,则MP+PQ+QN最小值是$\sqrt{10}$.