题目内容
5.若平行四边形的对角线长度分别为6和8,一边长为2x-1,则x的取值范围为( )| A. | 0<x<4 | B. | 1<x<4 | C. | 0<x<3 | D. | 1<x<3 |
分析 由平行四边形的性质得出OA=$\frac{1}{2}$AC=3,OB=$\frac{1}{2}$BD=4,在△AOB中,由两边之和大于第三边,两边之差小于第三边,得出不等式,解不等式即可.
解答 解:如图所示:
∵四边形ABCD是平行四边形,
∴OA=$\frac{1}{2}$AC=3,OB=$\frac{1}{2}$BD=4,
在△AOB中,4-3<AB<4+3,
∴1<2x-1<7,
解得:1<x<4;
故选:B.
点评 本题考查了平行四边形的性质、三角形的三边关系定理、不等式的解法;熟练掌握平行四边形的性质和三角形的三边关系定理是解决问题的关键.

练习册系列答案
相关题目
16.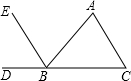 如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
 如图,若∠A=75°,则要使EB∥AC可添加的条件是( )
如图,若∠A=75°,则要使EB∥AC可添加的条件是( )| A. | ∠C=75° | B. | ∠DBE=75° | C. | ∠ABE=75° | D. | ∠EBC=105° |
10.用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )
| A. | 有一个内角小于90° | B. | 有一个内角小于或等于90° | ||
| C. | 每一个内角都小于90° | D. | 每一个内角都大于90° |
14.从图1到图2的变化过程可以发现的代数结论是( )
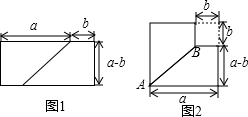

| A. | (a+b)(a-b)=a2-b2 | B. | a2-b2=(a+b)(a-b) | C. | (a+b)2=a2+2ab+b2 | D. | a2+2ab+b2=(a+b)2 |
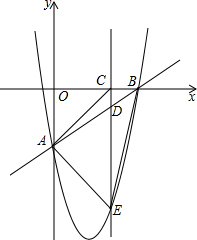 如图,在平面直角坐标系xOy中,直线y=x+m与坐标轴y轴交于点A,与x轴交于点B,过A,B两点的抛物线y=x2+nx-8,点D为线段AB上一动点,过点D作CD垂直x轴于点C,交抛物线于点E.
如图,在平面直角坐标系xOy中,直线y=x+m与坐标轴y轴交于点A,与x轴交于点B,过A,B两点的抛物线y=x2+nx-8,点D为线段AB上一动点,过点D作CD垂直x轴于点C,交抛物线于点E.
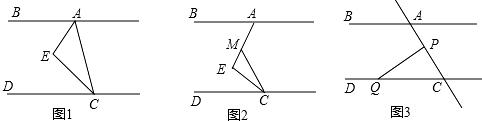
 如图,已知△ABC中,CD⊥AB于点D,若AB=5,BC=4,∠BCD=30°,求AC的长.
如图,已知△ABC中,CD⊥AB于点D,若AB=5,BC=4,∠BCD=30°,求AC的长.