题目内容
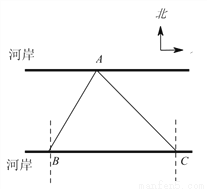
如图，要测量A点到河岸BC的距离，在B点测得A点在B点的北偏东30°方向上，在C点测得A点在C点的北偏西45°方向上，又测得BC=150m.求A点到河岸BC的距离.（结果保留整数）（参考数据：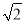 
≈1.41， 
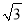≈1.73）
95m.
【解析】如图，过点A做AD⊥BC于点D，则AD的长为点A到河岸BC的距离.由题意知∠BAD=30°，∠CAD=45°，
∴在Rt△ADC中，CD =AD,
在Rt△ABD中,BD=ADtan30°，
∵BD+CD=150
∴AD+ADtan30°=150
即解得（m）
答：A点到BC的距离是95 m.
捷径训练检测卷系列答案
小夫子全能检测系列答案抛物线y＝ax2＋bx＋c的图象如图所示，则它关于y轴对称的抛物线的解析式是____．
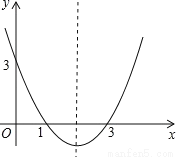
y＝x2＋4x＋3
【解析】∵点(1,0),(3,0),(0,3)关于y轴的对称点是(?1,0),(?3,0),(0,3).
则a?b+c=0，9a?3b+c=0，c=3联立方程组解得：a=1，b=4，c=3.
∴y=x²+4x+3；
方法二：由题意可知,抛物线y=x2+bx+c经过(1,0),(3,0),(0,3).
∴y=x²?4x+3.
∴关于y轴对称的抛... 当x=_______时，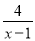 
与 
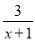的值相等．
-7
【解析】由题意得： = ，
解得：x=-7，
经检验x=-7是方程的解，
故答案为：-7. 把8米长的钢筋，焊成一个如图所示的框架，使其下部为矩形，上部为半圆形.请你写出钢筋所焊成框架的面积y(平方米)与半圆的半径x(米)之间的函数关系式.
y=－(π+2)x2+8x
【解析】分析：如图可求出半圆的面积以及一个长方形面积,然后可求出y与x之间的函数关系式.
本题解析：
半圆面积： πx2.
长方形面积： ×2x(8－2x－πx)=8x－(2+π)x2.
∴y=πx2+8x－(2+π)x2,
即y=－(π+2)x2+8x, 平时我们在跳绳时，绳摇到最高点处的形状可近似地看做抛物线，如图所示．正在摇绳的甲、乙两名同学拿绳的手间距为4 m，距地高均为1 m，学生丙、丁分别站在距甲拿绳的手水平距离1 m，2．5 m处．绳子在摇到最高处时刚好通过他们的头顶．已知学生丙的身高是1．5 m，则学生丁的身高为 ( )
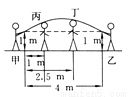
A. 1.5 m B. 1.625 m C. 1.66 m D. 1.67 m
B
【解析】设所求的函数的解析式为y=ax2+bx+c，由已知，函数的图象过（-1，1），（0，1.5），（3，1）三点，易求其解析式为y=-x2+x+,∵丁头顶的横坐标为1.5，∴代入其解析式可求得其纵坐标为1.625m.故选B. 一艘观光游船从港口A以北偏东60°的方向出港观光，航行60海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东30°方向，马上以40海里每小时的速度前往救援，海警船到达事故船C处所需的时间大约为_________小时（用根号表示）．
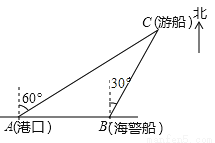
【解析】试题分析：过点C作CD⊥AB，则在Rt△ACD中，AC=60海里，∠CAD=30°可得：CD=30海里；在Rt△CBD中，∠CBD=60°，则BC=20海里，则t=20÷40=小时． 如图，小明同学在东西方向的环海路A处，测得海中灯塔P在北偏东60°方向上，在A处东500米的B处，测得海中灯塔P在北偏东30°方向上，则灯塔P到环海路的距离PC=（ ）米．
A. 250 B. 500 C. 250
D. 500
C
【解析】试题分析：设PC=x米，根据Rt△PBC的性质可得：BC=x米，根据Rt△PAC的性质可得：AC=x米，AB=AC-BC=x-x=500，解得：x=250米，故选C． 如图，在平行四边形ABCD中，若AB=6，AD=10，∠ABC的平分线交AD于点E，交CD的延长线于点F，求DF的长．
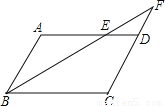
4
【解析】
试题分析：首先根据平行四边形的性质可得AB=DC=6，AD=BC=10，AB∥DC，再根据平行线的性质与角平分线的性质证明∠2=∠3，根据等角对等边可得BC=CF=10，再用CF﹣CD即可算出DF的长．
试题解析：∵四边形ABCD为平行四边形，∴AB=DC=6，AD=BC=10，AB∥DC． ∵AB∥DC，∴∠1=∠3，
又∵BF平分∠ABC，∴∠1=∠2，∴... 甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格有变化，两位采购员的购货方式也不同，其中，甲每次购买1000千克，乙每次用去800元，而不管购买多少饲料.
（1）甲、乙所购饲料的平均单价各是多少？
（2）谁的购货方式更合算？
（1）甲的平均单价为元/千克，乙平均单价为元/千克；（2）乙的购货方式更合算.
【解析】【试题分析】（1）设第一次饲料的价格为x元/千克，第二次饲料的价格为y元/千克，根据平均价格= ，代入即可.则这两次所购饲料的平均单价元/千克.则甲的平均单价为 元/千克；乙所购的饲料的平均单价为 元/千克.
(2)利用作差法比较大小即可.得： ，由于 ，得乙的购货方式更合算.
【试题解析...