题目内容
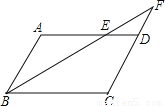
如图，在平行四边形ABCD中，若AB=6，AD=10，∠ABC的平分线交AD于点E，交CD的延长线于点F，求DF的长．
4
【解析】
试题分析：首先根据平行四边形的性质可得AB=DC=6，AD=BC=10，AB∥DC，再根据平行线的性质与角平分线的性质证明∠2=∠3，根据等角对等边可得BC=CF=10，再用CF﹣CD即可算出DF的长．
试题解析：∵四边形ABCD为平行四边形，∴AB=DC=6，AD=BC=10，AB∥DC． ∵AB∥DC，∴∠1=∠3，
又∵BF平分∠ABC，∴∠1=∠2，∴...
练习册系列答案
阅读快车系列答案
相关题目
抛物线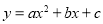
与x轴的两个交点为（﹣1，0），（3，0），其形状与抛物线
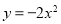相同，则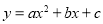的函数关系式为（ ）
A．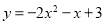
B．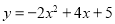
C．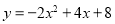
D．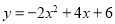
D．
【解析】
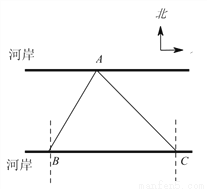
试题分析：由题意a=﹣2，∵抛物线与x轴的两个交点为（﹣1，0），（3，0）∴设y=﹣2（x+1）（x﹣3），即：．故选D． 如图，要测量A点到河岸BC的距离，在B点测得A点在B点的北偏东30°方向上，在C点测得A点在C点的北偏西45°方向上，又测得BC=150m.求A点到河岸BC的距离.（结果保留整数）（参考数据：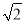 
≈1.41， 
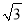≈1.73）
95m.
【解析】如图，过点A做AD⊥BC于点D，则AD的长为点A到河岸BC的距离.由题意知∠BAD=30°，∠CAD=45°，
∴在Rt△ADC中，CD =AD,
在Rt△ABD中,BD=ADtan30°，
∵BD+CD=150
∴AD+ADtan30°=150
即解得（m）
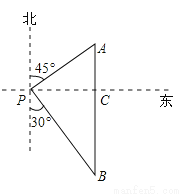
答：A点到BC的距离是95 m. 如图，一艘海轮位于灯塔P的东北方向，距离灯塔40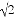
海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则海轮行驶的路程AB为（ ）海里．
A. 40+4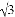0
B. 80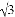 C. 40+2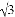0 D. 80
A
【解析】试题分析：根据题意可得：△APC为等腰直角三角形，则AC=PC=40海里，根据Rt△BCP的性质可得：BC=40海里，则AB=AC+BC=(40+40)海里，故选A． 如图，一艘海轮位于灯塔P的北偏东55°方向，距离灯塔2海里的点A处，如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB长是（ ）
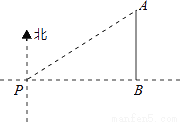
A. 2海里 B. 2sin55°海里 C. 2cos55°海里 D. 2tan55°海里
C
【解析】试题分析：首先由方向角的定义及已知条件得出∠NPA=55°，AP=2海里，∠ABP=90°，再由AB∥NP，根据平行线的性质得出∠A=∠NPA=55°．然后解Rt△ABP，得出AB=AP•cos∠A=2cos55°海里．
【解析】
如图，由题意可知∠NPA=55°，AP=2海里，∠ABP=90°．
∵AB∥NP，
∴∠A=∠NPA=55°．
在Rt△AB... 如图，在□ABCD中，AC，BD相交于点O，AB=10cm，AD=8cm，AC⊥BC，则OB= _________cm．
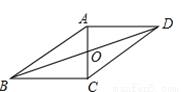
【解析】试题解析：∵四边形ABCD是平行四边形，
故答案为: ． 如图，平行四边形ABCD的对角线AC、BD相交于点O，下列结论正确的是（ ）
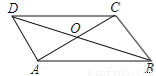
A．S□ABCD=4S△AOB
B．AC=BD
C．AC⊥BD
D．□ABCD是轴对称图形
A
【解析】
根据平行四边形的性质分别判断得出答案即可． 若一个多边形的边数增加1，则它的内角和增加 __________________
180°
【解析】设多边形边数为n，那么增加1条即为n+1，
原来内角和：(n-2)×180°=n×180°-360°，
现在内角和：(n+1-2)×180°=n×180°-180°，
内角和增加了180°，
故答案为：180°. 方程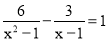
的解是( )
A. x=1 B. x=-4 C. x1=1,x2=-4 D. 以上答案都不
B
【解析】 .
故选B.