题目内容
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=( )米.

A. 250 B. 500 C. 250 D. 500
D. 500
 C
【解析】试题分析:设PC=x米,根据Rt△PBC的性质可得:BC=x米,根据Rt△PAC的性质可得:AC=x米,AB=AC-BC=x-x=500,解得:x=250米,故选C.
C
【解析】试题分析:设PC=x米,根据Rt△PBC的性质可得:BC=x米,根据Rt△PAC的性质可得:AC=x米,AB=AC-BC=x-x=500,解得:x=250米,故选C.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案已知二次函数的图象经过原点及点(-2,-2),且图象与x轴的另一个交点到原点的距离为4,那么该二次函数的解析式为___________
 或
【解析】∵图象与x轴的另一个交点到原点的距离为4,
∴这个交点坐标为(-4,0)、(4,0),
设二次函数解析式为,
①当这个交点坐标为(-4,0)时,
解得
所以二次函数解析式为
②当这个交点坐标为(4,0)时,
解得
所以二次函数解析式为
综上所述,二次函数解析式为或.
故答案为: 或
或
【解析】∵图象与x轴的另一个交点到原点的距离为4,
∴这个交点坐标为(-4,0)、(4,0),
设二次函数解析式为,
①当这个交点坐标为(-4,0)时,
解得
所以二次函数解析式为
②当这个交点坐标为(4,0)时,
解得
所以二次函数解析式为
综上所述,二次函数解析式为或.
故答案为: 或 分式方程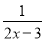 =l的解为 ( )
=l的解为 ( )
A. x=2 B. x=l C. x=-l D. x=-2
 A
【解析】方程两边同乘(2x-3),得
1=2x-3,
解得:x=2,
经检验,x=2是原方程的解,
故选A.
A
【解析】方程两边同乘(2x-3),得
1=2x-3,
解得:x=2,
经检验,x=2是原方程的解,
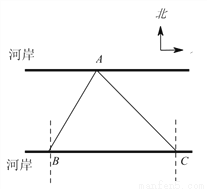
故选A. 如图,要测量A点到河岸BC的距离,在B点测得A点在B点的北偏东30°方向上,在C点测得A点在C点的北偏西45°方向上,又测得BC=150m.求A点到河岸BC的距离.(结果保留整数)(参考数据: 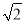 ≈1.41,
≈1.41, 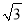 ≈1.73)
≈1.73)
 95m.
【解析】如图,过点A做AD⊥BC于点D,则AD的长为点A到河岸BC的距离.由题意知∠BAD=30°,∠CAD=45°,
∴在Rt△ADC中,CD =AD,
在Rt△ABD中,BD=ADtan30°,
∵BD+CD=150
∴AD+ADtan30°=150
即解得(m)
答:A点到BC的距离是95 m.
95m.
【解析】如图,过点A做AD⊥BC于点D,则AD的长为点A到河岸BC的距离.由题意知∠BAD=30°,∠CAD=45°,
∴在Rt△ADC中,CD =AD,
在Rt△ABD中,BD=ADtan30°,
∵BD+CD=150
∴AD+ADtan30°=150
即解得(m)
答:A点到BC的距离是95 m. 在我们生活中通常用两种方法来确定物体的位置.如小岛A在码头O的南偏东60°方向的14千米处,若以码头O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1千米为单位长度建立平面直角坐标系,则小岛A也可表示成____________
 (7,-7)
【解析】试题分析:过点A作AC⊥x轴于C,
在Rt△OAC中,∠AOC=90°-60°=30°,OA=14千米, 则AC=7千米,OC=7千米,
因而小岛A所在位置的坐标是(7,-7).
(7,-7)
【解析】试题分析:过点A作AC⊥x轴于C,
在Rt△OAC中,∠AOC=90°-60°=30°,OA=14千米, 则AC=7千米,OC=7千米,
因而小岛A所在位置的坐标是(7,-7). 如图,一艘海轮位于灯塔P的东北方向,距离灯塔40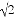 海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为( )海里.
海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为( )海里.
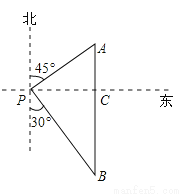
A. 40+40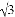 B. 80
B. 80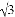 C. 40+20
C. 40+20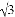 D. 80
D. 80
 A
【解析】试题分析:根据题意可得:△APC为等腰直角三角形,则AC=PC=40海里,根据Rt△BCP的性质可得:BC=40海里,则AB=AC+BC=(40+40)海里,故选A.
A
【解析】试题分析:根据题意可得:△APC为等腰直角三角形,则AC=PC=40海里,根据Rt△BCP的性质可得:BC=40海里,则AB=AC+BC=(40+40)海里,故选A. 如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
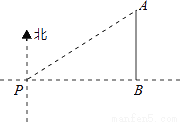
A. 2海里 B. 2sin55°海里 C. 2cos55°海里 D. 2tan55°海里
 C
【解析】试题分析:首先由方向角的定义及已知条件得出∠NPA=55°,AP=2海里,∠ABP=90°,再由AB∥NP,根据平行线的性质得出∠A=∠NPA=55°.然后解Rt△ABP,得出AB=AP•cos∠A=2cos55°海里.
【解析】
如图,由题意可知∠NPA=55°,AP=2海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=55°.
在Rt△AB...
C
【解析】试题分析:首先由方向角的定义及已知条件得出∠NPA=55°,AP=2海里,∠ABP=90°,再由AB∥NP,根据平行线的性质得出∠A=∠NPA=55°.然后解Rt△ABP,得出AB=AP•cos∠A=2cos55°海里.
【解析】
如图,由题意可知∠NPA=55°,AP=2海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=55°.
在Rt△AB... 如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是( )
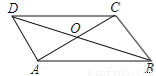
A.S□ABCD=4S△AOB
B.AC=BD
C.AC⊥BD
D.□ABCD是轴对称图形
 A
【解析】
根据平行四边形的性质分别判断得出答案即可.
A
【解析】
根据平行四边形的性质分别判断得出答案即可. 已知: 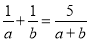 ,则
,则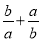 的值为_____.
的值为_____.
 3
【解析】根据,得: 将方程两边同时除以ab, =3.
故答案:3.
3
【解析】根据,得: 将方程两边同时除以ab, =3.
故答案:3. 
