题目内容
抛物线y＝ax2＋bx＋c的图象如图所示，则它关于y轴对称的抛物线的解析式是____．
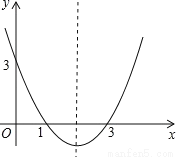
y＝x2＋4x＋3
【解析】∵点(1,0),(3,0),(0,3)关于y轴的对称点是(?1,0),(?3,0),(0,3).
则a?b+c=0，9a?3b+c=0，c=3联立方程组解得：a=1，b=4，c=3.
∴y=x²+4x+3；
方法二：由题意可知,抛物线y=x2+bx+c经过(1,0),(3,0),(0,3).
∴y=x²?4x+3.
∴关于y轴对称的抛...
冲刺100分单元优化练考卷系列答案在二次函数①y＝3x2；②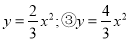
中，图象在同一水平线上的开口大小顺序用题号表示应该为( )
A. ①＞②＞③ B. ①＞③＞②
C. ②＞③＞① D. ②＞①＞③
C
【解析】根据二次函数的性质，可知系数a决定开口方向和开口大小，且a的值越大开口越小，因此可知②＞③＞①.
故选：C. 把抛物线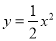
平移得到抛物线m，抛物线m经过点A（-6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线
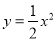交于点Q．
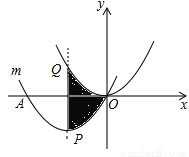
（1）求顶点P的坐标；
（2）写出平移过程；
（3）求图中阴影部分的面积．
（1）（-3， ）；（2）先向左平移3个单位，再向下平移个单位；（3）.
【解析】试题分析：（1）先利用交点式确定平移后的抛物线解析式，然后配成顶点式得到P点坐标；
（2）利用顶点的平移过程得到抛物线的平移过程；
（3）根据平移得到图中阴影部分的面积，然后根据三角形面积公式计算．
试题解析：（1）平移的抛物线解析式为= =，
所以顶点P的坐标为（-3， ）；
（... 王芳将如图所示的三条水平直线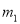
， 
， 
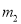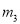的其中一条记为x轴（向右为正方向），三条竖直直线
， 
， 
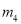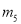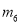的其中一条记为y轴（向上为正方向），并在此坐标平面内画出了抛物线
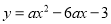，则她所选择的x轴和y轴分别为（ ）
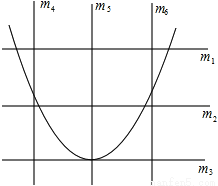
A.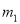 
， 
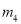
B.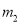 
， 
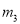
C.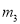 
， 
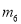
D.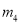 
， 
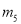
A
【解析】根据抛物线开口向上可知a＞0，将抛物线配方为，可得抛物线的对称轴为x=3，可知应选择的y轴为直线；由顶点坐标为（3，-3-9a），抛物线与y轴的交点为（0，-3），而-3-9a＜-3，可知应选择的x轴为直线，
故选：A． （8分）在平面直角坐标系xOy中，抛物线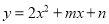
经过点A（0，-2）,B（3，4）．
（1）求抛物线的表达式及对称轴；
（2）设点B关于原点的对称点为C,点D是抛物线对称轴上一动点，记抛物线在A,B之间的部分为图像G（包含A,B两点）.若直线CD与图像G有公共点，结合函数图像，求点D纵坐标t 的取值范围．
（1）， （2）
【解析】试题分析：利用待定系数法求得解析式，再根据对称轴公式x=求得对称轴；画出图像找到D点的两个位置，进而求出范围.
试题解析：直线CD解析式：或y=-4 若抛物线经过点(3，0)和(2，－3)，且以直线x＝1为对称轴，则该抛物线的解析式为( )
A. y＝－x2－2x－3 B. y＝x2－2x＋3
C. y＝x2－2x－3 D. y＝－x2＋2x－3
C
【解析】设抛物线的解析式为：y=ax²+bx+c,把(3，0)和(2，－3)代入抛物线解析式得: ,
由直线x=1为对称轴,得到,即b=-2a,
代入方程组得: ,
解得:a=1,b=-2,c=-3 ,
则抛物线解析式为y=x²-2x-3,
所以C选项是正确的 已知二次函数的图象经过原点及点（-2，-2），且图象与x轴的另一个交点到原点的距离为4，那么该二次函数的解析式为___________
或
【解析】∵图象与x轴的另一个交点到原点的距离为4，
∴这个交点坐标为（-4，0）、（4，0），
设二次函数解析式为，
①当这个交点坐标为（-4，0）时，
解得
所以二次函数解析式为
②当这个交点坐标为（4，0）时，
解得
所以二次函数解析式为
综上所述，二次函数解析式为或．
故答案为： 或 抛物线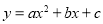
与x轴的两个交点为（﹣1，0），（3，0），其形状与抛物线
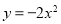相同，则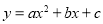的函数关系式为（ ）
A．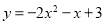
B．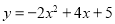
C．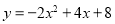
D．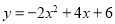
D．
【解析】
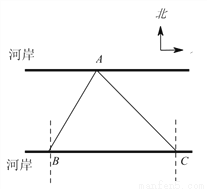
试题分析：由题意a=﹣2，∵抛物线与x轴的两个交点为（﹣1，0），（3，0）∴设y=﹣2（x+1）（x﹣3），即：．故选D． 如图，要测量A点到河岸BC的距离，在B点测得A点在B点的北偏东30°方向上，在C点测得A点在C点的北偏西45°方向上，又测得BC=150m.求A点到河岸BC的距离.（结果保留整数）（参考数据：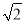 
≈1.41， 
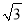≈1.73）
95m.
【解析】如图，过点A做AD⊥BC于点D，则AD的长为点A到河岸BC的距离.由题意知∠BAD=30°，∠CAD=45°，
∴在Rt△ADC中，CD =AD,
在Rt△ABD中,BD=ADtan30°，
∵BD+CD=150
∴AD+ADtan30°=150
即解得（m）
答：A点到BC的距离是95 m.