题目内容
把8米长的钢筋，焊成一个如图所示的框架，使其下部为矩形，上部为半圆形.请你写出钢筋所焊成框架的面积y(平方米)与半圆的半径x(米)之间的函数关系式.
y=－(π+2)x2+8x
【解析】分析：如图可求出半圆的面积以及一个长方形面积,然后可求出y与x之间的函数关系式.
本题解析：
半圆面积： πx2.
长方形面积： ×2x(8－2x－πx)=8x－(2+π)x2.
∴y=πx2+8x－(2+π)x2,
即y=－(π+2)x2+8x,
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
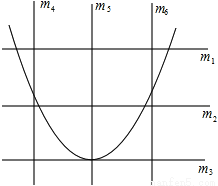
王芳将如图所示的三条水平直线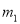
， 
， 
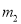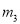的其中一条记为x轴（向右为正方向），三条竖直直线
， 
， 
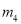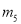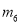的其中一条记为y轴（向上为正方向），并在此坐标平面内画出了抛物线
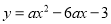，则她所选择的x轴和y轴分别为（ ）
A.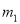 
， 
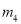
B.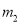 
， 
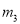
C.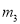 
， 
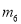
D.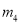 
， 
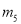
A
【解析】根据抛物线开口向上可知a＞0，将抛物线配方为，可得抛物线的对称轴为x=3，可知应选择的y轴为直线；由顶点坐标为（3，-3-9a），抛物线与y轴的交点为（0，-3），而-3-9a＜-3，可知应选择的x轴为直线，
故选：A． 抛物线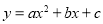
与x轴的两个交点为（﹣1，0），（3，0），其形状与抛物线
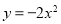相同，则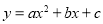的函数关系式为（ ）
A．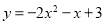
B．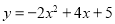
C．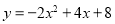
D．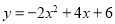
D．
【解析】
试题分析：由题意a=﹣2，∵抛物线与x轴的两个交点为（﹣1，0），（3，0）∴设y=﹣2（x+1）（x﹣3），即：．故选D． 方程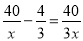
的解是______．
x=20
【解析】方程两边同时乘3x，得
120-4x=40，
解得：x=20，
检验：当x=20时，3x=60≠0，
所以x=20是原方程的根，
故答案为：x=20. 分式方程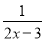
＝l的解为 ( )
A. x＝2 B. x＝l C. x＝-l D. x＝-2
A
【解析】方程两边同乘（2x-3），得
1=2x-3，
解得：x=2，
经检验，x=2是原方程的解，
故选A. 已知二次函数的图象开口向上，且顶点在y轴的负半轴上，请你写出一个满足条件的二次函数的表达式________．
y=x2-2
【解析】依题意,只要满足二次项系数为正数,顶点坐标为(0,k),k<0即可,
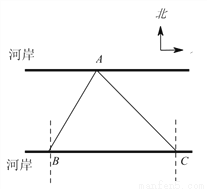
根据顶点式写解析式,本题答案不唯一,如y=x²-2.故答案为：y=x2-2. 如图，要测量A点到河岸BC的距离，在B点测得A点在B点的北偏东30°方向上，在C点测得A点在C点的北偏西45°方向上，又测得BC=150m.求A点到河岸BC的距离.（结果保留整数）（参考数据：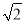 
≈1.41， 
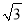≈1.73）
95m.
【解析】如图，过点A做AD⊥BC于点D，则AD的长为点A到河岸BC的距离.由题意知∠BAD=30°，∠CAD=45°，
∴在Rt△ADC中，CD =AD,
在Rt△ABD中,BD=ADtan30°，
∵BD+CD=150
∴AD+ADtan30°=150
即解得（m）
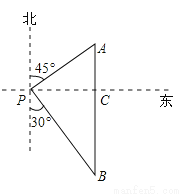
答：A点到BC的距离是95 m. 如图，一艘海轮位于灯塔P的东北方向，距离灯塔40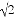
海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则海轮行驶的路程AB为（ ）海里．
A. 40+4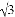0
B. 80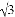 C. 40+2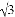0 D. 80
A
【解析】试题分析：根据题意可得：△APC为等腰直角三角形，则AC=PC=40海里，根据Rt△BCP的性质可得：BC=40海里，则AB=AC+BC=(40+40)海里，故选A． 若一个多边形的边数增加1，则它的内角和增加 __________________
180°
【解析】设多边形边数为n，那么增加1条即为n+1，
原来内角和：(n-2)×180°=n×180°-360°，
现在内角和：(n+1-2)×180°=n×180°-180°，
内角和增加了180°，
故答案为：180°.