题目内容
一艘观光游船从港口A以北偏东60°的方向出港观光，航行60海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东30°方向，马上以40海里每小时的速度前往救援，海警船到达事故船C处所需的时间大约为_________小时（用根号表示）．
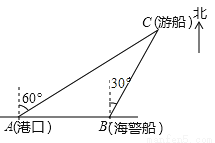
【解析】试题分析：过点C作CD⊥AB，则在Rt△ACD中，AC=60海里，∠CAD=30°可得：CD=30海里；在Rt△CBD中，∠CBD=60°，则BC=20海里，则t=20÷40=小时．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案若抛物线经过点(3，0)和(2，－3)，且以直线x＝1为对称轴，则该抛物线的解析式为( )
A. y＝－x2－2x－3 B. y＝x2－2x＋3
C. y＝x2－2x－3 D. y＝－x2＋2x－3
C
【解析】设抛物线的解析式为：y=ax²+bx+c,把(3，0)和(2，－3)代入抛物线解析式得: ,
由直线x=1为对称轴,得到,即b=-2a,
代入方程组得: ,
解得:a=1,b=-2,c=-3 ,
则抛物线解析式为y=x²-2x-3,
所以C选项是正确的 方程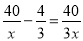
的解是______．
x=20
【解析】方程两边同时乘3x，得
120-4x=40，
解得：x=20，
检验：当x=20时，3x=60≠0，
所以x=20是原方程的根，
故答案为：x=20. 已知二次函数的图象开口向上，且顶点在y轴的负半轴上，请你写出一个满足条件的二次函数的表达式________．
y=x2-2
【解析】依题意,只要满足二次项系数为正数,顶点坐标为(0,k),k<0即可,
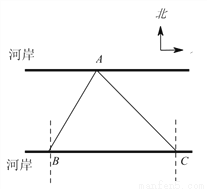
根据顶点式写解析式,本题答案不唯一,如y=x²-2.故答案为：y=x2-2. 如图，要测量A点到河岸BC的距离，在B点测得A点在B点的北偏东30°方向上，在C点测得A点在C点的北偏西45°方向上，又测得BC=150m.求A点到河岸BC的距离.（结果保留整数）（参考数据：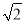 
≈1.41， 
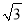≈1.73）
95m.
【解析】如图，过点A做AD⊥BC于点D，则AD的长为点A到河岸BC的距离.由题意知∠BAD=30°，∠CAD=45°，
∴在Rt△ADC中，CD =AD,
在Rt△ABD中,BD=ADtan30°，
∵BD+CD=150
∴AD+ADtan30°=150
即解得（m）
答：A点到BC的距离是95 m. 如图，甲、乙两船同时从港口O出发，其中甲船沿北偏西30°方向航行，乙船沿南偏西70°方向航行，已知两船的航行速度相同，如果1小时后甲、乙两船分别到达点A、B处，那么点B位于点A的（ ）
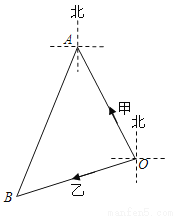
A. 南偏西40° B. 南偏西30° C. 南偏西20° D. 南偏西10°
C
【解析】试题分析：由甲船沿北偏西30°方向航行，乙船沿南偏西70°方向航行，得出∠BOA的度数，由两船的航行速度相同，得出AO=BO，得出∠BAO=50°，以及求出∠BAD的度数，得出点B位于点A的方向，故本题选C． 如图，一艘海轮位于灯塔P的东北方向，距离灯塔40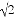
海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则海轮行驶的路程AB为（ ）海里．
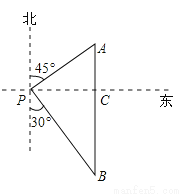
A. 40+4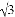0
B. 80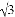 C. 40+2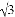0 D. 80
A
【解析】试题分析：根据题意可得：△APC为等腰直角三角形，则AC=PC=40海里，根据Rt△BCP的性质可得：BC=40海里，则AB=AC+BC=(40+40)海里，故选A． 如图，在□ABCD中，AC，BD相交于点O，AB=10cm，AD=8cm，AC⊥BC，则OB= _________cm．
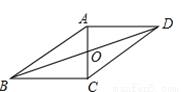
【解析】试题解析：∵四边形ABCD是平行四边形，
故答案为: ． 解分式方程：
（1）
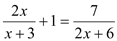
（2）
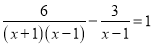
（1） （2）x=-4
【解析】【试题分析】（1）方程两边同时乘以 ，则 ；移项及合并得： 系数化为1： .经检验： 是原方程的根.
（2）方程两边同时乘以 ，去分母得： 去括号得： 移项得： 解得： 经检验，x=-4是原方程的根.
【试题解析】
方程两边同时乘以 ，则 ；
移项及合并得：
系数化为1： .
经检验： 是原方程的根.
方程两边同时乘以...