题目内容
15.阅读下列材料:问题:某饭店工作人员第一次买了13只鸡、5只鸭、9只鹅共用了925元.第二次买了2只鸡、4只鸭、3只鹅共用了320元,试问第三次买了鸡、鸭、鹅各一只共需多少元?(假定三次购买鸡、鸭、鹅的单价不变).
解:设鸡、鸭、鹅的单价分别为x、y、z元.依题意得:$\left\{\begin{array}{l}{13x+5y+9z=925}\\{2x+4y+3z=320}\end{array}\right.$
上述方程组可变形为:$\left\{\begin{array}{l}{5(x+y+z)+4(2x+z)=925}\\{4(x+y+z)-(2x+z)=320}\end{array}\right.$
设x+y+z=a,2x+z=b,上述方程组又可化为:$\left\{\begin{array}{l}{5a+4b=925①}\\{4a-b=320②}\end{array}\right.$
①+4×②得:a=105
即x+y+z=105
答:第三次买鸡、鸭、鹅各一只共需105元.
阅读后,细心的你,可以解决下列问题:
(1)上述材料中a=105
(2)选择题:上述材料中的解答过程运用了A思想方法来指导解题.
A、整体 B、数形结合 C、分类讨论
(3)某校体育组购买体育用品甲、乙、丙、丁的件数和用钱金额如下表:
| 品名次数 | 甲 | 乙 | 丙 | 丁 | 用钱金额(元) |
| 第一次购买件数 | 5 | 4 | 3 | 1 | 1882 |
| 第二次购买件数 | 9 | 7 | 5 | 1 | 2764 |
分析 (1)按要求补充完整上面求解过程,即可得知a=105;
(2)在(1)解题过程中:设x+y+z=a,2x+z=b是运用了整体思想方法来解决问题的,由此得知选A;
(3)设体育组所购买的体育用品甲、乙、丙、丁的单价分别为x、y、z、m元.根据题意列出关于x、y、z、m的四元一次方程组,将方程组进行变形,设“x+y+z+m=a,4x+3y+2z=b”将四元一次方程组变为二元一次方程组,解方程组即可得出x+y+z+m的值.
解答 解:(1)按照解方程的过程补充完整解题过程如下:
问题:某饭店工作人员第一次买了13只鸡、5只鸭、9只鹅共用了925元.第二次买了2只鸡、4只鸭、3只鹅共用了320元,试问第三次买了鸡、鸭、鹅各一只共需多少元?(假定三次购买鸡、鸭、鹅的单价不变).
解:设鸡、鸭、鹅的单价分别为x、y、z元.依题意得:$\left\{\begin{array}{l}{13x+5y+9z=925}\\{2x+4y+3z=320}\end{array}\right.$
上述方程组可变形为:$\left\{\begin{array}{l}{5(x+y+z)+4(2x+z)=925}\\{4(x+y+z)-(2x+z)=320}\end{array}\right.$
设x+y+z=a,2x+z=b,上述方程组又可化为:$\left\{\begin{array}{l}{5a+4b=925①}\\{4a-b=320②}\end{array}\right.$
①+4×②得:a=105,
即x+y+z=105,
答:第三次买鸡、鸭、鹅各一只共需,105元.
故答案为:105.
(2)(1)的解题过程中:设x+y+z=a,2x+z=b,
是运用了整体思想解决问题.
故选A.
(3)设体育组所购买的体育用品甲、乙、丙、丁的单价分别为x、y、z、m元.
根据题意得:$\left\{\begin{array}{l}{5x+4y+3z+m=1882}\\{9x+7y+5z+m=2764}\end{array}\right.$,
该方程组可变形为:$\left\{\begin{array}{l}{(x+y+z+m)+(4x+3y+2z)=1882}\\{(x+y+z+m)+2(4x+3y+2z)=2764}\end{array}\right.$,
设x+y+z+m=a,4x+3y+2z=b,
上述方程组又可化为:$\left\{\begin{array}{l}{a+b=1882}\\{a+2b=2764}\end{array}\right.$,
解得:a=1000.
即x+y+z+m=1000.
答:购买每种体育用品各一件共需1000元.
点评 本题考查了二元一次方程组的应用以及利用换元法解方程组,解题的关键是:(1)根据解方程过程补充完整解题步骤;(2)运用了整体思想解决问题;(3)利用换元法得出关于a、b的二元一次方程组.本题属于基础题,难度不大,解决该题型题目时,整体替换部分是关键.

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
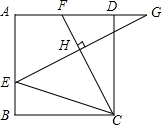 如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )
如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )| A. | 1:1 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1:2 |
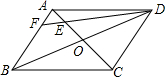 如图,?ABCD的对角线AC,BD相交于点O,点E是AO的中点,连接DE并延长交AB于点F,请探究AF与BF的数量关系,并证明你的结论.
如图,?ABCD的对角线AC,BD相交于点O,点E是AO的中点,连接DE并延长交AB于点F,请探究AF与BF的数量关系,并证明你的结论.