题目内容
4.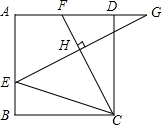 如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )
如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )| A. | 1:1 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1:2 |
分析 由四边形ABCD是正方形,得到∠B=∠ADC=∠BCD=∠CDG=90°,BC=CD,推出△BCE≌△CDG,根据全等三角形的性质得到∠1=∠2,CE=CG,证得△ECG是等腰直角三角形,根据等腰直角三角形的性质得到CH=EH=HG,通过△FGH∽△AGE,根据相似三角形的性质即可得到结论.
解答 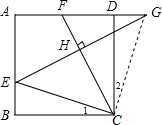 解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴∠B=∠ADC=∠BCD=∠CDG=90°,BC=CD,
在△BCE与△CDG中,
$\left\{\begin{array}{l}{BC=CD}\\{∠B=∠CDG}\\{BE=DG}\end{array}\right.$,
∴△BCE≌△CDG,
∴∠1=∠2,CE=CG,
∴∠ECG=90°,
∴△ECG是等腰直角三角形,
∵CF⊥EG,
∴CH=EH=HG,
∵AB=AD=3,BE=CD=1,
∴AE=2,AG=4,
∵∠A=∠GHF=90°,∠FGH=∠AGE,
∴△FGH∽△AGE,
∴$\frac{FH}{CH}=\frac{AE}{AG}=\frac{2}{4}=\frac{1}{2}$,
∴$\frac{FH}{CH}$=$\frac{1}{2}$.
故选D.
点评 本题考查了相似三角形的判定和性质.正方形的性质,全等三角形的判定和性质,连接CG构造全等三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.阅读下列材料:
问题:某饭店工作人员第一次买了13只鸡、5只鸭、9只鹅共用了925元.第二次买了2只鸡、4只鸭、3只鹅共用了320元,试问第三次买了鸡、鸭、鹅各一只共需多少元?(假定三次购买鸡、鸭、鹅的单价不变).
解:设鸡、鸭、鹅的单价分别为x、y、z元.依题意得:$\left\{\begin{array}{l}{13x+5y+9z=925}\\{2x+4y+3z=320}\end{array}\right.$
上述方程组可变形为:$\left\{\begin{array}{l}{5(x+y+z)+4(2x+z)=925}\\{4(x+y+z)-(2x+z)=320}\end{array}\right.$
设x+y+z=a,2x+z=b,上述方程组又可化为:$\left\{\begin{array}{l}{5a+4b=925①}\\{4a-b=320②}\end{array}\right.$
①+4×②得:a=105
即x+y+z=105
答:第三次买鸡、鸭、鹅各一只共需105元.
阅读后,细心的你,可以解决下列问题:
(1)上述材料中a=105
(2)选择题:上述材料中的解答过程运用了A思想方法来指导解题.
A、整体 B、数形结合 C、分类讨论
(3)某校体育组购买体育用品甲、乙、丙、丁的件数和用钱金额如下表:
那么,购买每种体育用品各一件共需多少元?
问题:某饭店工作人员第一次买了13只鸡、5只鸭、9只鹅共用了925元.第二次买了2只鸡、4只鸭、3只鹅共用了320元,试问第三次买了鸡、鸭、鹅各一只共需多少元?(假定三次购买鸡、鸭、鹅的单价不变).
解:设鸡、鸭、鹅的单价分别为x、y、z元.依题意得:$\left\{\begin{array}{l}{13x+5y+9z=925}\\{2x+4y+3z=320}\end{array}\right.$
上述方程组可变形为:$\left\{\begin{array}{l}{5(x+y+z)+4(2x+z)=925}\\{4(x+y+z)-(2x+z)=320}\end{array}\right.$
设x+y+z=a,2x+z=b,上述方程组又可化为:$\left\{\begin{array}{l}{5a+4b=925①}\\{4a-b=320②}\end{array}\right.$
①+4×②得:a=105
即x+y+z=105
答:第三次买鸡、鸭、鹅各一只共需105元.
阅读后,细心的你,可以解决下列问题:
(1)上述材料中a=105
(2)选择题:上述材料中的解答过程运用了A思想方法来指导解题.
A、整体 B、数形结合 C、分类讨论
(3)某校体育组购买体育用品甲、乙、丙、丁的件数和用钱金额如下表:
| 品名次数 | 甲 | 乙 | 丙 | 丁 | 用钱金额(元) |
| 第一次购买件数 | 5 | 4 | 3 | 1 | 1882 |
| 第二次购买件数 | 9 | 7 | 5 | 1 | 2764 |
 如图,把一个长方形纸条ABCD沿EF折叠,若∠BGE=112°,则∠1=56°.
如图,把一个长方形纸条ABCD沿EF折叠,若∠BGE=112°,则∠1=56°.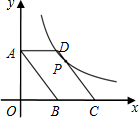 如图,给定的点A,B分别在y轴正半轴、x轴正半轴上,延长OB至点C,使BC=OB,以AB,BC为邻边构造?ABCD,点P从点D出发沿边DC向终点C运动(点P不与点C重合),反比例函数的图象y=$\frac{k}{x}$经过点P,则k的值的变化情况是( )
如图,给定的点A,B分别在y轴正半轴、x轴正半轴上,延长OB至点C,使BC=OB,以AB,BC为邻边构造?ABCD,点P从点D出发沿边DC向终点C运动(点P不与点C重合),反比例函数的图象y=$\frac{k}{x}$经过点P,则k的值的变化情况是( )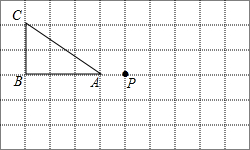 如图,将△ABC绕点O顺时针旋转180°后得到△A′B′C′.请画出旋转后的△A′B′C′.
如图,将△ABC绕点O顺时针旋转180°后得到△A′B′C′.请画出旋转后的△A′B′C′. 如图,在等腰直角三角形ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,Rt△PMN的直角顶点P在线段AB上,PM、PN分别交于AC、BC于点E、F,PA:PB=1:2,∠BPF=15°,则EF的长为$\frac{2\sqrt{30}}{3}$.
如图,在等腰直角三角形ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,Rt△PMN的直角顶点P在线段AB上,PM、PN分别交于AC、BC于点E、F,PA:PB=1:2,∠BPF=15°,则EF的长为$\frac{2\sqrt{30}}{3}$.